Question

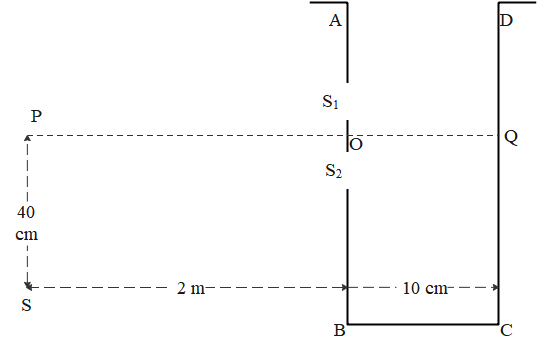
A vessel ABCD of 10 cm width has two small slits ${{S}_{1}}$ and ${{S}_{2}}$ sealed with identical glass plates of equal thickness. The distance between slits is 0.8 mm. PQ is the line perpendicular to the plane AB and passing through O, the middle point of ${{S}_{1}}$ and ${{S}_{2}}$. A monochromatic light source is kept at S, 40 cm below P and 2 m from the vessel, to illuminate the slits as shown in the figure below. Calculate the position of the central bright fringe on the other wall CD with respect to the line OQ. Now, a liquid is poured into the vessel and filled up to OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid.

Answer 1

Hint: This question is related to Young’s double slit experiment. Central maxima is obtained, when the path difference between two coherent waves is zero. Use this concept, to derive a relation for distance of central bright fringe from Q. When liquid is introduced, path length passing from liquid increases by a multiple of refractive index. Use this fact, to obtain an expression for the position of the central bright fringe after liquid is introduced. Then solve the equation for refractive index.

Formula used: For central fringe in double slit experiment, path difference $\Delta z=0$

Complete step by step answer:
We assume that central fringe is formed at distance ${{x}_{2}}$ from Q. Let us assume this position to be R. Since path difference for central fringe is zero, therefore
$\left( S{{S}_{1}}+{{S}_{1}}R \right)-\left( S{{S}_{2}}+{{S}_{2}}R \right)=0$
$\left( S{{S}_{1}}-S{{S}_{2}} \right)=\left( {{S}_{2}}R-{{S}_{1}}R \right)$
Using Pythagoras theorem, in triangle $\text{SB}{{\text{S}}_{\text{1}}}\text{, SB}{{\text{S}}_{\text{2}}}\text{,}\,{{\text{S}}_{\text{1}}}\text{RQ}\,\text{and}\,{{\text{S}}_{\text{2}}}\text{RQ}$ we get
${{\left( S{{S}_{1}} \right)}^{2}}={{D}_{1}}^{2}+{{\left( {{x}_{1}}+\dfrac{d}{2} \right)}^{2}}\Rightarrow S{{S}_{1}}^{2}={{D}_{1}}^{2}{{\left( 1+\dfrac{{{x}_{1}}+\dfrac{d}{2}}{{{D}_{1}}} \right)}^{2}}$
${{\left( S{{S}_{2}} \right)}^{2}}={{D}_{1}}^{2}+{{\left( {{x}_{1}}-\dfrac{d}{2} \right)}^{2}}\Rightarrow {{\left( S{{S}_{2}} \right)}^{2}}={{D}_{1}}^{2}{{\left( 1+\dfrac{{{x}_{1}}-\dfrac{d}{2}}{{{D}_{1}}} \right)}^{2}}$
${{\left( {{S}_{1}}R \right)}^{2}}={{D}_{2}}^{2}+{{\left( {{x}_{2}}-\dfrac{d}{2} \right)}^{2}}$
${{\left( {{S}_{2}}R \right)}^{2}}={{D}_{2}}^{2}+{{\left( {{x}_{2}}-\dfrac{d}{2} \right)}^{2}}$
We have assumed ${{\text{S}}_{\text{1}}}\text{RQ}\,\text{and}\,{{\text{S}}_{\text{2}}}\text{RQ}$ as right-angled triangle as ${{S}_{1}}Q={{S}_{2}}Q=\dfrac{d}{2}$ is very small and can be neglected.

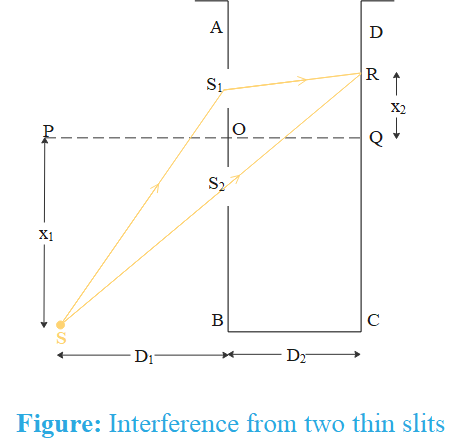
Now, we assume that ${{D}_{1}}\gg {{x}_{1}},d$ and ${{D}_{2}}\gg {{x}_{2}},d$, then
$S{{S}_{1}}={{D}_{1}}{{\left( 1+\dfrac{{{x}_{1}}^{2}+{{x}_{1}}d+\dfrac{{{d}^{2}}}{4}}{{{D}_{1}}^{2}} \right)}^{\dfrac{1}{2}}}\approx {{D}_{1}}+\dfrac{x_{1}^{2}}{2{{D}_{1}}}+\dfrac{{{x}_{1}}d}{2{{D}_{1}}}+\dfrac{{{d}^{2}}}{8{{D}_{1}}}$
Similarly,
$S{{S}_{2}}={{D}_{1}}{{\left( 1+\dfrac{{{x}_{1}}^{2}-{{x}_{1}}d+\dfrac{{{d}^{2}}}{4}}{{{D}_{1}}^{2}} \right)}^{\dfrac{1}{2}}}\approx {{D}_{1}}+\dfrac{x_{1}^{2}}{2{{D}_{1}}}-\dfrac{{{x}_{1}}d}{2{{D}_{1}}}+\dfrac{{{d}^{2}}}{8{{D}_{1}}}$
$\Rightarrow S{{S}_{1}}-S{{S}_{2}}=\dfrac{{{x}_{1}}d}{{{D}_{1}}}$
In a similar way, we obtain
${{S}_{2}}R-{{S}_{1}}R=\dfrac{{{x}_{2}}d}{{{D}_{2}}}$
$\because \left( S{{S}_{1}}-S{{S}_{2}} \right)=\left( {{S}_{2}}R-{{S}_{1}}R \right)$
$\therefore \dfrac{{{x}_{1}}d}{{{D}_{1}}}=\dfrac{{{x}_{2}}d}{{{D}_{2}}}\Rightarrow {{x}_{2}}=\dfrac{{{D}_{2}}}{{{D}_{1}}}{{x}_{1}}$
Substituting the values of ${{D}_{1}}=2m=200cm;\,{{D}_{2}}=10cm;\,\text{and }{{x}_{1}}=40cm$, we have
${{x}_{2}}=\dfrac{10}{200}\times 40=2cm$
When liquid is poured into the vessel and filled up to OQ, the central fringe shifts to Q. For the central fringe to be at Q, Path difference must be zero.
$\left( S{{S}_{1}}+{{S}_{1}}Q \right)-\left( S{{S}_{2}}+\mu \,{{S}_{2}}Q \right)=0$
$\Rightarrow S{{S}_{1}}-S{{S}_{2}}=\mu {{S}_{2}}Q-{{S}_{1}}Q$
$\Rightarrow \dfrac{{{x}_{1}}d}{{{D}_{1}}}\approx \mu {{\left( {{D}_{2}}^{2}+\dfrac{{{d}^{2}}}{4} \right)}^{1/2}}-{{\left( {{D}_{2}}^{2}+\dfrac{{{d}^{2}}}{4} \right)}^{1/2}}=\left( \mu -1 \right){{\left( {{D}_{2}}^{2}+\dfrac{{{d}^{2}}}{4} \right)}^{1/2}}$
$\dfrac{{{x}_{1}}d}{{{D}_{1}}}=(\mu -1){{D}_{2}}\left( 1+\dfrac{{{d}^{2}}}{4{{D}_{2}}^{2}} \right)\approx (\mu -1){{D}_{2}}$
Substituting the values, we get
$\dfrac{40cm\times 0.08cm}{200cm}=(\mu -1)\times 10cm$
$\Rightarrow \mu =1.0016$

The refractive index of liquid is 1.0016.

Note: The path length of the wave changes to $\mu$ index times its path length in free space when it passes through a material of refractive index $\mu$.
In this question, values of different lengths are given in different units. When using these values in formula, they must be changed to the same unit first.