Question

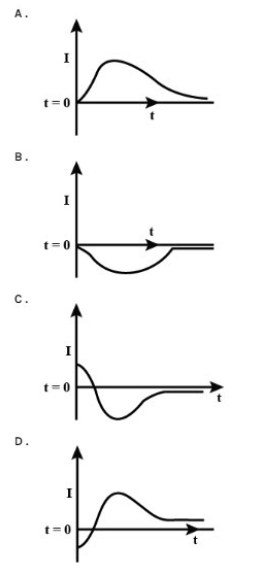
A very long solenoid of radius R is carrying current I(t)=kte-αt(k>0), as a function of time (t≥0). counter clockwise current is taken to be positive. A circular conducting coil of radius 2Ris placed in the equatorial plane of the solenoid and concentric with the solenoid. The current induced in the outer coil is correctly depicted, as a function of time, by?

Answer 1

Hint: As we all know that mutual inductance tells us about the relation between flux and current It tells us about the relation between the flux of object 2 and the current of object 1 and self inductance tells us about the flux of object 1 with respect to the current of object 2.

Formula used: $I(t) = kt{e^{ - \alpha t}}$

Complete step by step answer:
We can see that the current $I$ is the function of time. Since from the given curves, it can be seen that the current is zero at a point of time and also the initial value of the current is zero.

We all know that the flux change in the ring is due to the current inside the solenoid.Therefore, the flux through the ring is given by,

$\eqalign{
  & {\phi _2} = M{i_1} \cr
  & {\phi _2} = Mkt{e^{ - \alpha t}} \cr} $

Here, ${\phi _2}$is the flux of a ring and ${i_1}$ is the current through the solenoid and $M$ is the mutual inductance. Now we can say that due to change in flux inside the ring an emf is also generated inside the ring. So we can say that the value of emf is given by,

$emf = - \dfrac{{d{\phi _2}}}{{dt}}$…… (I)

We will substitute ${\phi _2} = Mkt{e^{ - \alpha t}}$in equation (I) to find the value of emf.

$\eqalign{
  & emf = - \dfrac{{d\left( {Mkt{e^{ - \alpha t}}} \right)}}{{dt}} \cr
  & emf = - Mk\left( {1 - \alpha t} \right){e^{ - \alpha t}} \cr} $

Now we all know that current generated inside the ring is given by,

${i_2} = \dfrac{{emf}}{R}$…… (II)

We will now substitute the value of $emf = - Mk\left( {1 - \alpha t} \right){e^{ - \alpha t}}$to find the value of current through coil that is ${i_2}$. Therefore, it becomes,

${i_2} = \dfrac{{ - Mk\left( {1 - \alpha t} \right){e^{ - \alpha t}}}}{R}$

When the value of $t$ becomes $t = \dfrac{1}{\alpha }$ then at that point the current becomes,
$\eqalign{
  & {i_2} = \dfrac{{ - Mk\left( {1 - \alpha \times \dfrac{1}{\alpha }} \right){e^{ - \alpha t}}}}{R} \cr
  & {i_2} = 0 \cr} $

Now at $t = 0$, we can find the initial value of current. So we will put $t = 0$ and it becomes,

$\eqalign{
  & {i_2} = \dfrac{{ - Mk\left( {1 - \alpha \times 0} \right){e^{ - \alpha \times 0}}}}{R} \cr
  & {i_2} = \dfrac{{ - Mk}}{R} \cr} $

So we can come to the point that, on seeing the behaviour of current a $t = 0$ and $t = \dfrac{1}{\alpha }$
So, the correct answer is “Option D”.
In option (D), the initial value of the current is negative and it is also zero somewhere in the time axis.

Additional Information:
We know that when the current passes through the solenoid it generates the magnetic field inside the solenoid. And as the magnetic lines of force also crosses the ring of radius $2R$, it generates a change in flux inside the ring.

Note:
We know that the relation between magnetic field and current is determined by the Biot savart law. The constant current generated by the magnetic field is given by the biot savart law. It gives the relation between the magnetic field and current magnitude, length, direction and proximity.