Question

A vertical wire carries a current in upward direction. If an electron beam sent horizontally towards the wire, then it will be deflected:
A. Vertically downwards and perpendicular to the plane of the paper
B. Vertically upwards and perpendicular the plane of the paper
C. Vertically upwards and in the plane of the paper
D. No deflection

Answer 1

Hint: Remember that a current carrying conductor produces a magnetic field. First determine the direction of the magnetic field at the electron beam. Then determine the direction of the force acting on this moving beam as a consequence of the magnetic field impending on it either quantitatively or by Fleming’s left hand rule. In both cases, remember to account for the negative charge of the electron beam.

Formula used:
The force exerted by a magnetic field on a moving charge $\vec{F} = q(\vec{v} \times \vec{B})$, where q is the charge of the moving charge, v is the velocity of the moving charge, and B is the magnetic field acting on the moving charge.

Complete answer:
We first begin with a vertical wire carrying current in the upward direction. Therefore, from the right hand thumb rule, we determine that the magnetic field produced flows around this wire in an anticlockwise direction.
We then have an electron beam that is incident horizontally towards the wire as shown in the figure. Therefore, the velocity vector points leftwards, in the negative x-axis direction $= v(-\hat{i})$

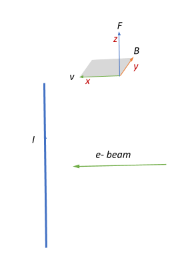
Now the magnetic field of the wire at the electron beam is directed into the plane of the paper. Let this be along the y-axis $= B \hat{j}$
Therefore, the force exerted by this magnetic field on the electron beam can be obtained:
$\vec{F} = q(\vec{v} \times \vec{B})$ where q is the electric charge of the beam, v is the velocity of the beam, and B is the magnetic field of the beam. We take the charge of the electron to be $-q$
$\Rightarrow \vec{F} = (-q)(v(-\hat{i}) \times B(\hat{j})) = - (-\hat{k}) = \hat{k}$
Therefore, the force acts in the z direction and deflects the electron beam upwards and in the plane of the paper (x-z plane).

So, the correct answer is “Option C”.

Note:
An alternate way to obtain the direction in which the force that deflects the beam is exerted without any evaluation is by using the Right Hand Thumb Rule to determine the direction of the magnetic field produced by the current carrying wire, and then to use Fleming’s Left Hand Rule to determine the direction of the force that is exerted on the beam as a consequence of B acting on the beam. In this method, remember to account for the negative charge of the electron, which will change the direction of the force that you get from the left hand rule.