Question

(A) Using Bohr’s second postulate of quantization of orbit angular momentum shows that the circumference of the electron in the nth orbital state in hydrogen atom is n times the de-Broglie wavelength associated with it.
(B) The electron in a hydrogen atom initially in the third excited state. What is the maximum number of spectral lines which can be emitted when it finally moves to the ground state?

Answer 1

Hint: Recall Bohr’s second postulate of quantization which states that, an electron revolves around the nucleus in orbits and the angular momentum of revolution is an integral multiple of $\dfrac{h}{{2p}}$, where $h$ is the planck’s constant. Recall the formula for finding total number of possible spectral lines.

Formula used:
According to Bohr’s second postulate of quantization,
$mv{r_n} = n\dfrac{h}{{2\pi }}$
Where, $m$ is the mass of the electron revolving around the nucleus
$v$ is the velocity of electron in permitted quantized orbit
${r_n}$ is the radius of the orbit
$n$ is the principal quantum number ($n = 1,2,3....$)
$h$ is the planck's constant
Total number of possible spectral line,
$N = \dfrac{{n(n - 1)}}{2}$
Where, $n$ is the value for the excited state

Complete step by step solution:
(A) According to Bohr’s second postulate of quantization,
$mv{r_n} = n\dfrac{h}{{2\pi }}$
On cross multiplication we get,
$ \Rightarrow 2\pi {r_n} = \dfrac{{nh}}{{mv}}$
We know that, $p = mv$
On putting this in the above equation, we get
$ \Rightarrow 2\pi {r_n} = n\dfrac{h}{p}$ ………(i)
Now, according to the de-broglie hypothesis,
$\lambda = \dfrac{h}{p}$ …………(ii)
Where, $\lambda $ is the wavelength associated electron
From equation (i) and (ii) we get
$ \Rightarrow 2\pi {r_n} = n\lambda $

Hence, it is shown that the circumference of the electron in the nth orbital state in hydrogen atom is n times the de-Broglie wavelength associated with it.

(B) It is given in the question that the electron in the hydrogen atom is initially in the third excited state.
As we know that, for ground state $n = 1$
So, for third excited state, $n = 4$
Now, the total number of possible spectral lines is given by the formula,
$N = \dfrac{{n(n - 1)}}{2}$
On putting $n = 4$ in the above equation, we get
$ \Rightarrow N = \dfrac{{4(4 - 1)}}{2}$
On further solving that, we get
$N = 6$
Hence possible transitions are shown in figure below

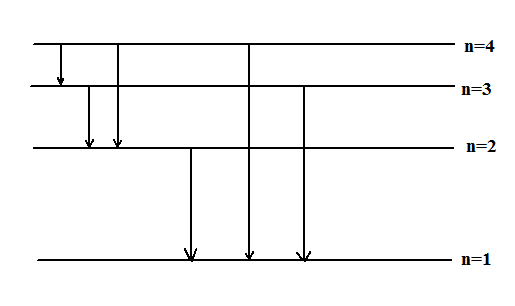
Therefore, the maximum number of spectral lines is 6.

Note: According to the Bohr’s third postulate, an electron can transition from a non-radiating orbit to another of a lower energy level. In doing so, a photon is emitted whose energy is equal to the energy difference between the two states. When the electron is revolving in an orbit closest to the nucleus, the energy of the atom is the least or has the largest negative value.