Question

A uniformly charged rod of length 4cm and linear charge density \[\lambda = 30{\rm{ }}\mu {{\rm{C}} {\left/{\vphantom {{\rm{C}} {\rm{m}}}} \right.} {\rm{m}}}\] is placed as shown in figure. Calculate the x-component of electric field at point P

Answer 1

Hint:We will use the expression for electric field in x-direction of the rod which gives us the relation between linear charge density, vertical distance between point P and rod, Coulomb’s constant and angles made by electric field with the vertical.

Complete step by step answer:
Given:
The length of rod is \[l = 4{\rm{ cm}} \times \left( {\dfrac{{\rm{m}}}{{100{\rm{ cm}}}}} \right) = 0.04{\rm{ m}}\].
The distance between rod and point P is \[r = 3{\rm{ cm}} = 3{\rm{ cm}} \times \left( {\dfrac{{\rm{m}}}{{100{\rm{ cm}}}}} \right) = 0.03{\rm{ m}}\].
The linear charge density is \[\lambda = 30{\rm{ }}\mu {{\rm{C}} {\left/
{\vphantom {{\rm{C}} {\rm{m}}}} \right.
} {\rm{m}}}\].
We have to calculate the x-component of electric point P.
Let us write the general expression for the electric field in the x-direction of rod.
\[{E_x} = \dfrac{{k\lambda }}{r}\left( {\cos {\theta _1} - \cos {\theta _2}} \right)\]……(1)
Here k is the Coulomb’s constant for air, \[{\theta _1}\] is the angle at point P and
\[{\theta _2}\] is the angle at another point Q if it exists in negative y-direction in a similar fashion as that of P.
We know that the value of Coulomb’s constant is given as:
\[k = 9 \times {10^9}{\rm{ N}} \cdot {{{{\rm{m}}^2}} {\left/
{\vphantom {{{{\rm{m}}^2}} {{{\rm{C}}^2}}}} \right.
} {{{\rm{C}}^2}}}\]
Let us redraw the above figure as below:

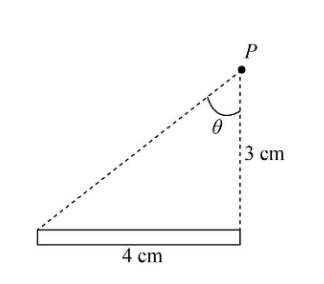
From the given figure we can conclude that point Q is not present in our problem so we can substitute zero for \[{\theta _2}\].
We can use the tangent of angle \[\theta \] to find its value from the above diagram.
\[
\tan \theta = \left( {\dfrac{{{\rm{4 cm}}}}{{3{\rm{ cm}}}}} \right)\\
= \dfrac{4}{3}
\]
Taking the inverse of tangent on both sides of the above expression, we get:
\[
\theta = {\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right)\\
= 53.13^\circ
\]
On substituting \[9 \times {10^9}{\rm{ N}} \cdot {{{{\rm{m}}^2}} {\left/
{\vphantom {{{{\rm{m}}^2}} {{{\rm{C}}^2}}}} \right.
} {{{\rm{C}}^2}}}\] for k, \[30{\rm{ }}\mu {{\rm{C}} {\left/
{\vphantom {{\rm{C}} {\rm{m}}}} \right.
} {\rm{m}}}\] for \[\lambda \], \[0.03{\rm{ m}}\] for r \[53.13^\circ \] for \[{\theta _1}\] and \[0^\circ \] for \[{\theta _2}\] in equation (1), we get:
\[
{E_x} = \dfrac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{{{\rm{m}}^2}} {\left/
{\vphantom {{{{\rm{m}}^2}} {{{\rm{C}}^2}}}} \right.
} {{{\rm{C}}^2}}}} \right)\left( {30{\rm{ }}\mu {{\rm{C}} {\left/
{\vphantom {{\rm{C}} {\rm{m}}}} \right.
} {\rm{m}}}} \right)}}{{0.03{\rm{ m}}}}\left( {\cos 53.13^\circ - \cos 0^\circ } \right)\\
= \dfrac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{{{\rm{m}}^2}} {\left/
{\vphantom {{{{\rm{m}}^2}} {{{\rm{C}}^2}}}} \right.
} {{{\rm{C}}^2}}}} \right)\left( {30 \times {{10}^{ - 6}}{{\rm{C}} {\left/
{\vphantom {{\rm{C}} {\rm{m}}}} \right.
} {\rm{m}}}} \right)}}{{0.03{\rm{ m}}}}\left( {\cos 53.13^\circ - \cos 0^\circ } \right)\\
= - 36 \times {10^5}{\rm{ }}{{\rm{N}} {\left/
{\vphantom {{\rm{N}} {\rm{C}}}} \right.
} {\rm{C}}}
\]
Therefore, we can write that the value of electric field in x-direction is \[ - 36 \times {10^5}{\rm{ }}{{\rm{N}} {\left/{\vphantom {{\rm{N}} {\rm{C}}}} \right.} {\rm{C}}}\].

Note:The negative value of electric field signifies that the direction of electric field is opposite to our consideration. Also, we should not be confused with the value of \[{\theta _2}\] as it is not present in our problem so we can substitute it equal to zero.