Question

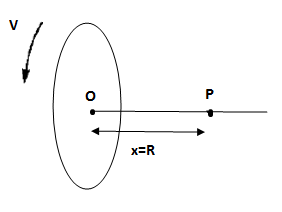
A uniformly charged ring of radius R is rotated about its axis with constant linear speed v of its particles. The ratio of electric field to magnetic field at a point P on the axis of the ring distant x=R from the centre of ring is:

(A)\[\dfrac{{{c}^{2}}}{v}\]
(B)$\dfrac{{{v}^{2}}}{c}$
(C)$\dfrac{v}{c}$
(D) $\dfrac{c}{v}$

Answer 1

Hint: In the problem it is given that the charged ring is rotated about its own axis. This will cause a current to flow. Then we calculate the electric field at a point P from the ring. Next we calculate the magnetic field due to the current flowing through the ring at the point P from the ring. Taking the ratio of electric to magnetic field, we find the correct answer.

Formula used: The electric field due to a charge q on a ring of radius R at a distance x is given by
E=$\dfrac{qx}{4\pi {{\varepsilon }_{0}}{{({{R}^{2}}+{{x}^{2}})}^{\dfrac{3}{2}}}}$
The magnetic field due to a ring at point P due to the rotating current that produces current i,
B= $\dfrac{{{\mu }_{0}}i{{R}^{2}}}{2{{({{R}^{2}}+{{x}^{2}})}^{\dfrac{3}{2}}}}$

Complete answer:
Given,
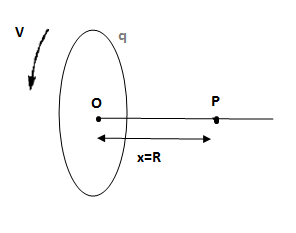
Distance from centre of the ring to point P in the figure, x =R
Let the charge on the ring be q
The electric field due to the rotating ring at a point P is given by

E=$\dfrac{qx}{4\pi {{\varepsilon }_{0}}{{({{R}^{2}}+{{x}^{2}})}^{\dfrac{3}{2}}}}$
Where q is the charge on the ring
x is the distance of the point P from the centre of the ring
R id the radius of the ring
$\because $ x=R
Plugging this value in equation (1), we have
E=$\dfrac{qR}{4\pi {{\varepsilon }_{0}}{{({{R}^{2}}+{{R}^{2}})}^{\dfrac{3}{2}}}}$
$\begin{align}
  & \Rightarrow E=\dfrac{qR}{4\pi {{\varepsilon }_{0}}{{(2R)}^{\dfrac{3}{2}}}} \\
 & \Rightarrow E=\dfrac{q}{4\pi {{\varepsilon }_{0}}\times 2\sqrt{2}{{R}^{2}}} \\
\end{align}$
Thus the electric field at point P due to the ring is given by $E=\dfrac{q}{4\pi {{\varepsilon }_{0}}\times 2\sqrt{2}{{R}^{2}}}$ …….(1)
Now to calculate the magnetic field, we have
Let $\omega $ be the angular velocity of the rotating ring.
$\therefore $ f=$\dfrac{\omega }{2\pi }$
And let the current produced be, i=$\dfrac{q}{t}$
$\begin{align}
  & \Rightarrow i=qf \\
 & \Rightarrow i=q\dfrac{\omega }{2\pi } \\
\end{align}$ ……… (2)
Due to the rotation of the ring, there is a current flow in the wire which produces a magnetic field.
The magnetic field at a point P due to current i
B=$\dfrac{{{\mu }_{0}}i{{R}^{2}}}{2{{({{R}^{2}}+{{x}^{2}})}^{\dfrac{3}{2}}}}$
Plugging x=R and putting the value of equation (2) in the above equation, we have
B=$\dfrac{{{\mu }_{0}}\dfrac{q\omega }{2\pi }{{R}^{2}}}{2{{({{R}^{2}}+{{R}^{2}})}^{\dfrac{3}{2}}}}$
Putting the value of $\omega =\dfrac{v}{R}$ , where v is the given velocity of the rotating ring
$\Rightarrow B=\dfrac{{{\mu }_{0}}qv}{4\pi 2\sqrt{2}R}$
$\therefore $ The magnetic field at point P due to the rotating ring is given by$B=\dfrac{{{\mu }_{0}}qv}{4\pi 2\sqrt{2}R}$ ………..(3)
Taking the ratio of (1) to (3), we have the ratio of electric to magnetic field as
$\begin{align}
  & \dfrac{E}{B}=\dfrac{\dfrac{q}{4\pi {{\varepsilon }_{0}}2\sqrt{2}{{R}^{2}}}}{\dfrac{{{\mu }_{0}}qv}{4\pi 2\sqrt{2}{{R}^{2}}}} \\
 & \Rightarrow \dfrac{E}{B}=\dfrac{1}{{{\mu }_{0}}{{\varepsilon }_{0}}}\times \dfrac{1}{v} \\
 & \Rightarrow \dfrac{E}{B}=\dfrac{{{c}^{2}}}{v}(\because \dfrac{1}{\sqrt{{{\mu }_{0}}{{\varepsilon }_{0}}}}=c) \\
\end{align}$
Thus from the above calculations, it is clear that the ratio of electric to magnetic field at a distance P is given by $\dfrac{{{c}^{2}}}{v}$.

So, the correct answer is “Option A”.

Additional Information:
While solving this problem, we see that the electric field due to a ring is because of charge on the ring. On the other hand, the magnetic field on the ring is primarily due to the electric current flowing through the ring. Thus it is clear that for a body to create a magnetic field, charges must necessarily be in motion.

Note:
In the above problem, care must be taken while calculating the electric field and the magnetic field at a distance x from the centre of the ring. The formula must be kept in mind otherwise deriving it takes time which can be saved otherwise.