Question

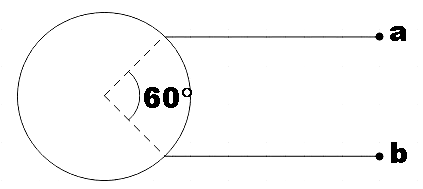
A uniform wire of resistance $18\Omega $ is bent in the form of a circle. The effective resistance across the points $a$ and $b$ is:

A. $3\Omega $
B. $2\Omega $
C.$2.5\Omega $
D. $6\Omega $

Answer 1

Hint: As a first step, you could divide the full circle into two resistors of different resistances. You could then find the combination formed by them across the terminals. Then, you could find the resistance of arc that subtends $1{}^\circ $ at the centre and thereby the resistances of the arcs that subtends $60{}^\circ $ and $300{}^\circ $ at the centre. After that you could find the effective resistance of the combination.

Formula used:
Effective resistance of resistors connected in parallel,
${{R}_{eff}}=\dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$

Complete Step by step solution:
In the question, we are given a uniform wire of resistance $18\Omega $. This wire is being bent in the form of a circle. If two terminals $a$ and $b$ are connected at points that subtend $60{}^\circ $ at the centre of the circle then, we are asked to find the effective resistance across the terminals $a$ and $b$.

We see that the terminals divide the circle into two arcs, one bigger than the other. Let the resistance of the bigger arc be ${{R}_{1}}$ and let the resistance of the smaller arc be ${{R}_{2}}$, then, it would be equivalent to two resistors connected in parallel to each other.

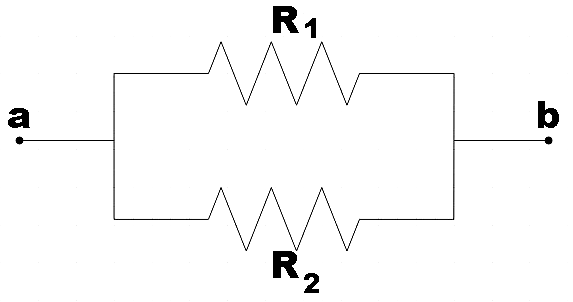
So the effective resistance would be given by,
${{R}_{eff}}=\dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$ ………………………………………………………. (1)

Now let us find the resistances of each resistor, that is, each arc.
The whole circle is said to have a resistance of$18\Omega $.
$360{}^\circ \to 18\Omega $
$\Rightarrow 1{}^\circ \to \dfrac{18}{360}\Omega $

As the bigger arc subtends $300{}^\circ $ at the centre of the circle, its resistance would be given by,
${{R}_{1}}=\dfrac{18}{360}\times 300=15\Omega $ …………………………………………… (2)

Now the smaller arc subtends $60{}^\circ $ and its resistance could be given by,
${{R}_{2}}=\dfrac{18}{360}\times 60=3\Omega $…………………………………………… (3)

Substituting (2) and (3) in (1), we get,
${{R}_{eff}}=\dfrac{15\times 3}{15+3}$
$\therefore {{R}_{eff}}=2.5\Omega $

Therefore, we found the effective resistance across the terminals to be,
${{R}_{eff}}=2.5\Omega $

Hence, option C is found to be the correct answer.

Note:
Chances are there that you may get the combination formed by the arcs wrong. This happens because the arcs are seen to form continuous circles and this may appear to be connected in series. But the terminals are actually connected in parallel as their two ends are connected at the two terminals.