Question

A uniform thin bar of mass 6m and length 2l is bent to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is:
\[A.\,\,\dfrac{5}{9}m{{l}^{2}}\]
\[B.\,\,5m{{l}^{2}}\]
\[C.\,\,4m{{l}^{2}}\]
\[D.\,\,\dfrac{1}{12}m{{l}^{2}}\]

Answer 1

Hint: In this problem, as the hexagon was earlier a uniform thin bar, so the formula for calculating the moment of inertia of the rod should be used. In this case, the total moment of inertia is the sum of moment of inertia at the centre and moment of inertia at the perpendicular distance.
Formula used:
\[I=\dfrac{m{{L}^{2}}}{12}\]

Complete answer:
From given, we have,
The mass of a thin bar = 6m
The length of a thin bar = 2l
As the length of the uniform thin bar is 2l, the length of each segment of the hexagon will be,
\[\dfrac{2l}{6}=\dfrac{l}{3}\]
The moment of inertia of a rod is given by the formula,
\[I=\dfrac{m{{L}^{2}}}{12}\]
Where m is the mass of the rod and L is the length of the rod.
Substitute the values of the mass and length of the rod in the above equation. So, we get,
\[\begin{align}
  & I=\dfrac{1}{12}(6m){{\left( \dfrac{l}{3} \right)}^{2}} \\
 & \Rightarrow I=\left( \dfrac{6m}{12} \right)\left( \dfrac{{{l}^{2}}}{9} \right) \\
 & \Rightarrow I=\dfrac{6m{{l}^{2}}}{108} \\
 & \Rightarrow I=\dfrac{m{{l}^{2}}}{18} \\
\end{align}\]
The distance between the centre of the hexagon and the centre of the rod is calculated as,

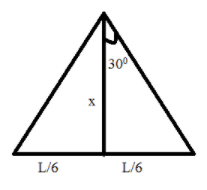
Let x be the distance between the centre of the hexagon and the centre of the rod.
\[\begin{align}
  & \tan 30{}^\circ =\dfrac{{}^{l}/{}_{6}}{x} \\
 & \dfrac{l}{6x}=\dfrac{1}{\sqrt{3}} \\
 & x=\dfrac{\sqrt{3}l}{6} \\
\end{align}\]
Using the parallel axis theorem the moment of inertia about the axis is,
\[\begin{align}
  & I'=\dfrac{m{{l}^{2}}}{18}+6m{{\left( \dfrac{\sqrt{3}l}{6} \right)}^{2}} \\
 & \Rightarrow I'=\dfrac{m{{l}^{2}}}{18}+6m\left( \dfrac{3{{l}^{2}}}{36} \right) \\
 & \Rightarrow I'=\dfrac{m{{l}^{2}}}{18}+\dfrac{3m{{l}^{2}}}{6} \\
 & \Rightarrow I'=\dfrac{m{{l}^{2}}}{18}+\dfrac{m{{l}^{2}}}{2} \\
 & \Rightarrow I'=\dfrac{5}{9}m{{l}^{2}} \\
\end{align}\]
As the moment of inertia of a uniform thin bar about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is equal to \[\dfrac{5}{9}m{{l}^{2}}\].

Thus, the option (A) is correct.

Note:
The things to be on your finger-tips for further information on solving these types of problems are: The distance between the centre of the hexagon and the centre of the rod should be calculated cautiously, as this part also becomes important to find the total moment of inertia.