Question

A uniform rod of length L and mass M is held vertical with its bottom end pivoted to the floor. The rod falls under gravity, freely turning about the pivot. If acceleration due to gravity is g, what is the instantaneous angular speed of the rod when it makes an angle $60^o$ with the vertical
A. ${{\left( \dfrac{g}{L} \right)}^{{1}/{2}\;}}$
B. ${{\left( \dfrac{3g}{4L} \right)}^{{1}/{2}\;}}$
C. $\sqrt{3gl}$
D. ${{\left( \dfrac{3g}{2L} \right)}^{{1}/{2}\;}}$

Answer 1

Hint: Use law of conservation of energy i.e. the total energy of an isolated system remains constant. In this problem as the uniform rod has maximum potential energy at initial position but when it starts falling then the potential energy is converted into kinetic energy.

Formula used:
According to conservation of energy:
Loss in potential energy = Gain in kinetic Energy
$Mgh=\dfrac{1}{2}I{{\omega }^{2}}$
$I$ about the end = $\dfrac{M{{L}^{2}}}{3}$
Where $M$- mass of the rod
$h$- height of centre of gravity
$I$- moment of inertia
$\omega $ - angular speed

Complete step-by-step answer:
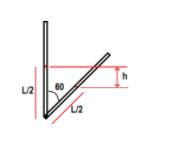
Firstly, find the height from which centre of gravity fall:
$\begin{align}
  & h=\dfrac{L}{2}\cos {{60}^{\circ }} \\
 & \Rightarrow h=\dfrac{L}{4} \\
\end{align}$

Now, decrease in potential energy of the system:
$Mgh=\dfrac{MgL}{4}$
Kinetic energy of the system:
$\begin{align}
  & K.E=\dfrac{1}{2}I{{\omega }^{2}} \\
 & \Rightarrow K.E=\dfrac{1}{2}\left( \dfrac{M{{L}^{2}}}{3} \right){{\omega }^{2}} \\
\end{align}$
Applying conservation of energy:
Potential energy = Kinetic energy
$\begin{align}
  & Mgh=K.E \\
 & \Rightarrow \dfrac{MgL}{4}=\dfrac{1}{2}\left( \dfrac{M{{L}^{2}}}{3} \right){{\omega }^{2}} \\
 & \Rightarrow \omega ={{\left( \dfrac{3g}{2L} \right)}^{{1}/{2}\;}} \\
\end{align}$

So, the correct answer is “Option D”.

Additional Information: The conservation of energy may be a fundamental concept of physics alongside the conservation of mass and therefore the conservation of momentum. Within some problem domain, the quantity of energy remains constant and energy is neither created nor destroyed. Energy is often converted from one form to a different form (potential energy is often converted to kinetic energy) but the entire energy within the domain remains fixed.

Note: A consequence of the law of conservation of energy is that a motion machine of the primary kind cannot exist, that's to mention, no system without an external energy supply can deliver a vast amount of energy to its surroundings. So just take care about the system on which you are applying the law of conservation of energy and then the second thing the height of centre of gravity should be calculated carefully.