Question

A uniform magnetic field of $1.5$ T exists in a cylindrical region of radius $10$cm, its direction being parallel to the axis along east to west. A current carrying ire in north-south direction passes through the region. The wire intersects the axis and experiences a force of $1.2$ N downwards. If the wire is turned north-south to northeast-southwest direction, the magnitude and the direction of force is
a) $1.2$ N, upwards
b) $1.2\sqrt{2}$ N, downward
c)$1.2$ N, downwards
d)$\dfrac{1.2}{\sqrt{2}}$ N, downwards

Answer 1

Hint: The wire in the region of the magnetic field will only experience force. Hence while turning, the length of wire in the magnetic will increase. Further compare the two conditions to obtain the force on the wire when it's turned.

Complete solution:
Let us understand the concept right hand rule for two vectors perpendicular to each other

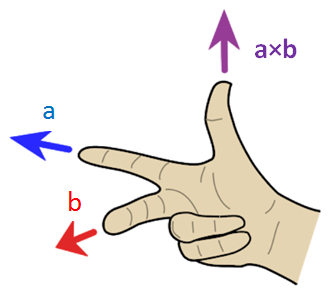
If we see the above diagram, if there are two vectors a and b represented by the middle and the forefinger of your right hand, then its cross product is given by the thumb.

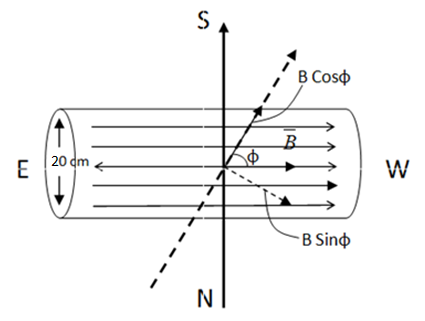
So if we see the above diagram, initially the wire carries current from north to south and the magnetic field is in east-west direction. Using right hand rule the direction of the force is found to be upwards. It is to be noted that the wire of length only 20 cm experiences force.
When the wire is turned in the northeast-southwest direction the length of the wire in the magnetic field changes. The length of the wire now in magnetic field is,
Using trigonometric definition of Sine i.e. from the above diagram
$\operatorname{Sin}\Phi =\dfrac{\text{Opposite}}{\text{Hypotenuse}}$
Opposite equal to $20$ cm (denoted as L )and hypotenuse is the required length of the wire
Hence length of wire is $\dfrac{L}{\operatorname{Sin}\Phi }$
Force on any current carrying wire is given by
$\overline{F}=i(l\times B)$
In the above equation 1
$l$ is a length vector directed towards the direction of current,
$i$ is the value of electric current,
B is the value of magnetic field
The above equation can also be written as
$\overline{F}=ilB\operatorname{Sin}\Phi $ where $\Phi $is the angle between $l$ and$B$
Let us assume the current carried by the wire is $i$ and length be $l$
In the first case the wire was perpendicular to the magnetic field. Therefore force on the wire is,
$\overline{F}=ilB\operatorname{Sin}90$
Since $\operatorname{Sin}90=1$
$\overline{F}=ilB$
It is given that $\overline{F}=1.2N$ and $B=1.5T$, hence the above equation can be written as,
$1.2=il1.5$
Let us name this as equation 2

In the second case the wire is turned in northeast-southwest direction let us say at an angle $\Phi $hence using equation 1 the force in this case become,
$\overline{F}=ilB\operatorname{Sin}\Phi $
Since $B=1.5T$and length=$\dfrac{L}{\operatorname{Sin}\Phi }$the above equation reduces to,
$\overline{F}=i\dfrac{L}{\operatorname{Sin}\Phi }1.5\operatorname{Sin}\Phi $
$\overline{F}=il1.5$
If we consider equation 2, the magnitude of force experienced is the same.
Hence the force on the wire is 1.2N.
Speaking about the direction the component of magnetic field $B\operatorname{Sin}\Phi $ makes an angle 90 with the wire and using right hand thumb rule again the direction of the force is downwards.

Hence, the correct answer to the question is option a.

Note:
Do not use the left hand to figure out the direction of the force. The perpendicular magnetic field only contributes to the force on the conductor. The horizontal component of the magnetic field being parallel does not have its effect on the moving charges inside the conductor.