Question

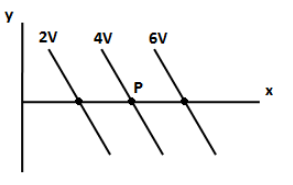
A uniform electric field exists in the (x-y) plane and some equipotential lines are shown below. A positively charged particle is released from point P. Its velocity vector will be (a and b are positive constants)

A. \[a\hat i\]
B. \[a\hat i + b\hat j\]
C. \[a\hat i - b\hat j\]
D. \[ - a\hat i - b\hat j\]

Answer 1

Hint: The three lines have shown in the above figure shows that the potential remains the same along these lines. The force acting on the charged particle in the electric field is the electric force. For the positive charge, the direction of electric force is the same as the direction of electric field.

Formula used:
Electric force, \[{\vec F_e} = q\vec E\]
Here, \[\vec E\] is the electric field and q is the charge.

Complete step by step answer:
We know that the equipotential surface is the region where the potential remains constant. The three lines shown in the above figure shows that the potential remains the same along the line. We can see in the above figure, the potential increases along the x-axis. We know that the difference in potential creates electric fields and the direction of electric field is from the higher potential to the lower potential.
The electric field is a vector quantity. The direction of the electric field will not be along the negative x-axis but it should be perpendicular to the equipotential lines since the potential remains constant perpendicular to the electric field.
Now, we release a positively charged particle at point P. We know that the only force that will act on the particle is the electric force. We have the expression for electric force,
\[{\vec F_e} = q\vec E\]
Here, \[\vec E\] is the electric field and q is the charge.
Since the charge is positive, the direction of electric force must be along the direction of the electric field. We can denote the velocity vector of the positive charge as shown in the figure below.

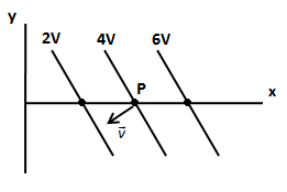
Thus, the velocity vector of the charged particle in the above figure can be expressed as,
\[\therefore\vec v = a\hat i - b\hat j\]

So, the correct answer is option C.

Note: If instead of a positively charged particle, we release a negatively charged particle, the direction of the electric force will be opposite to the direction of the electric field. Therefore, the negatively charged particle would have moved in the opposite direction of the electric field because the negative charge attracts towards the higher potential.