Question

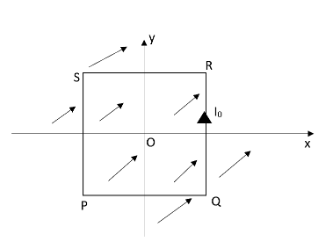
A uniform, constant magnetic field B directed at an angle of $45{}^\circ $ to the x-axis in the x-y plane. PQRS is a rigid, square wire frame carrying a steady current ${{I}_{0}}$​, with its centre at the origin O. At time $t=0$, the frame is at rest in the position shown in figure, with its sides parallel to the x- and y-axes. Each side of the frame is of mass $M$ and length $L$. If the angle by which the frame rotates under the action of this torque in a short interval of time $\Delta t$, and the axis about which this rotation occurs is $\theta =\dfrac{3}{X} \& \dfrac{{{I}_{0}}B}{M}\Delta {{t}^{2}}$. Find X? Given, moment of inertia of the frame about an axis through its centre perpendicular to its plane is $\left(\dfrac{4}{3} \right)M{{L}^{2}}$.

$\begin{align}
  & A.\dfrac{3}{7}\dfrac{{{I}_{0}}B}{M}\Delta {{t}^{2}} \\
 & B.\dfrac{3}{4}\dfrac{{{I}_{0}}B}{M}\Delta {{t}^{2}} \\
 & C.\dfrac{3}{2}\dfrac{{{I}_{0}}B}{M}\Delta {{t}^{2}} \\
 & D.\dfrac{3}{5}\dfrac{{{I}_{0}}B}{M}\Delta {{t}^{2}} \\
\end{align}$

Answer 1

Hint: This question is solved using the perpendicular axes theorem. The perpendicular axis theorem says that a planar lamina is having a moment of inertia about an axis which is perpendicular to the plane of the lamina will be equivalent to the sum of the moments of inertia of the lamina around the two axes at the right angles to each other where the perpendicular axis passes through it. Here the equations of circular motion will be valid.

Complete answer:
The moment of inertia of the frame about QS using the theorem of perpendicular axis,
${{I}_{QS}}=\dfrac{1}{2}{{I}_{Z}}=\dfrac{1}{2}\left( \dfrac{4}{3}M{{L}^{2}} \right)=\dfrac{2}{3}M{{L}^{2}}$
As we all know, the angular acceleration is given as,
$\tau =I\alpha $
Rearranging the equation will give,
$\alpha =\dfrac{\tau }{I}$
Where $\tau $ be the torque and $I$be the moment of inertia.
$\alpha =\dfrac{\tau }{I}=\dfrac{3{{I}_{0}}{{L}^{2}}B}{2{{L}^{2}}M}$
Simplifying this equation will give the angular acceleration,
$\alpha =\dfrac{3{{I}_{0}}B}{2M}$
As we can see here the value of angular acceleration is constant. Therefore the equations of circular motion is applicable here.
Hence we can write that,
$\theta ={{\omega }_{0}}t+\dfrac{1}{2}\alpha {{t}^{2}}$
Where ${{\omega }_{0}}=0$.
Thus the angular acceleration will be,
$\theta =\dfrac{1}{2}\alpha {{t}^{2}}$
Substituting the value of angular acceleration in it,
$\theta =\dfrac{1}{2}\left( \dfrac{3{{I}_{0}}B}{2M} \right){{\left( \Delta t \right)}^{2}}=\dfrac{3}{4}\dfrac{{{I}_{0}}B}{M}\Delta {{t}^{2}}$

So, the correct answer is “Option B”.

Note:
Angular acceleration is defined as the variation in angular velocity divided by the time taken. There are two kinds of angular velocity. One is known as spin angular velocity and the other is known as orbital angular velocity.