Question

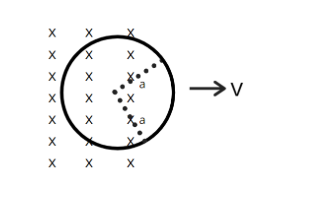
A uniform circular loop of radius a and resistance $R$  is pulled at a constant velocity $v$  out of a region of uniform magnetic field whose magnitude is $B$ . The plane of loop and the velocity are both perpendicular to $B$ . Then the electrical power in the circular loop at the instant when the arc (of circular loop) outside the region of magnetic field subtends an angle $\dfrac{\pi }{3}$ at centre of the loop is 

Answer 1

Hint: The concept of this question is based on electromagnetic induction and energy consideration and we are aware that lenz's law is consistent with the law of conservation of energy.

Complete step by step solution:
Given that,
Uniform circular loop of radius is = $a$
having resistance is = $R$
constant velocity is=$v$
magnitude of magnetic field is= $B$
and angle subtend is =$\dfrac{\pi }{3}$
We can see in the diagram, the loop is coming out of the magnetic field with a constant velocity $v$
Now calculate rate of change of the magnetic field,
 and area enclosed by the magnetic field. So,
 Area of circular loop $(A) = \pi {r^2}$
According to question $r = a$ ,
Now area become after putting $r$ as$a$,
Area $(A) = \pi {a^2}$ …………...(1)
\[
   = \left[ {\pi {a^2}\left( {\dfrac{{2\theta }}{{2\pi }}} \right) - \dfrac{x}{2}2a\sin \theta } \right] \\
   = \pi {a^2} - {a^2}\theta + ax\sin \theta \\
\]
\[ = \pi {a^2} - {a^2}{\cos ^{ - 1}}\left( {\dfrac{x}{a}} \right) + ax\sin \theta \]..............( 2)
Putting $ax\sin \theta $ =$ax\dfrac{{\sqrt {{x^2} - {a^2}} }}{a}$ ……………..( 3)
Putting value of (3) in (2) equation
We get,
$ = \pi {a^2} - {a^2}{\cos ^{ - 1}}\left( {\dfrac{x}{a}} \right) + ax\dfrac{{\sqrt {{x^2} - {a^2}} }}{a} $
Electromotive force given as
$\varepsilon = \dfrac{{d\phi }}{{dt}}$
The rate of change in the magnetic flux passing through the loop is
$\varepsilon = B\dfrac{{dA}}{{dt}}$
Now differentiate the area of loop,
$\dfrac{{dA}}{{dt}} = 0 + \dfrac{{{a^2}}}{{\sqrt {1 - \dfrac{{{x^2}}}{{{a^2}}}} }} \times \dfrac{1}{a}\dfrac{{dx}}{{dt}} + \left[ {\sqrt {{a^2} - {x^2}} - \dfrac{x}{2}\dfrac{{2x}}{{\sqrt {{x^2} - {a^2}} }}} \right]\dfrac{{dx}}{{dt}}$
Now do some basic calculation solve above equation,
As we now, $x = \dfrac{{\sqrt 3 a}}{2}$
We get, $\dfrac{{dA}}{{dt}} = av$ and
For electric power in the circular loop at the instant when the arc outside the region of magnetic field,
$ P = \dfrac{{{\varepsilon ^2}}}{R} \\
  P = {B^2} \times \dfrac{1}{R}{\left( {\dfrac{{dA}}{{dt}}} \right)^2} \\
  P = \dfrac{{{B^2}{a^2}{v^2}}}{R} \\
$

Hence, Electric power in the circular loop is $P = \dfrac{{{B^2}{a^2}{v^2}}}{R}$

Note:If the magnetic field is increasing, the induced field acts in the opposite direction but in the case we just take positive electromotive force because no opposition component is acting on the system.