Question

A triangle by the line $y = 0,{\text{ }}y = x{\text{ and }}x = 4$revolves about the $x$-axis. Find the volume of the solid of revolution.

Answer 1

Hint: - Draw the triangle using the given conditions first . Now, since this triangle is revolving around $x$-axis use the formula of volume of solid of revolution around $x$-axis that is $\int\limits_0^x {\pi {y^2}dx} $.

Complete step-by-step answer:

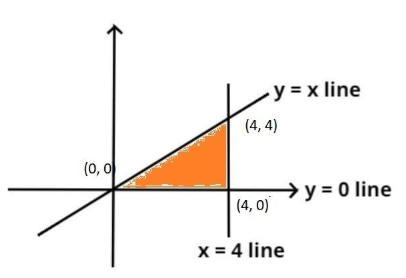
The pictorial representation of the lines $y = 0,{\text{ }}y = x{\text{ and }}x = 4$ is shown above.
Now it is given that$y = x$, so when $y = 0$
 $ \Rightarrow x = 0$
Now, when $x = 4$
$ \Rightarrow y = x = 4$
So the intersection point is $\left( {4,4} \right)$
Now, as we know that volume\[\left( V \right)\] of solid of revolution around $x$-axis is $\int\limits_0^x {\pi {y^2}dx} $
Now as we see integration is about x-axis so we have to put the integration limits of x.
So, the integration limit is from 0 to 4 because $x$is from 0 to 4.
$ \Rightarrow V = \int\limits_0^4 {\pi {y^2}dx} $
Now put $y = x$
$ \Rightarrow V = \int\limits_0^4 {\pi {x^2}dx} $
As, you know integration of$\int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}} + c$, where c is some arbitrary integration constant, so use this basic property of integration we have,
$ \Rightarrow V = \pi \left[ {\dfrac{{{x^3}}}{3}} \right]_0^4$
Now, apply integration limit
$ \Rightarrow V = \pi \left[ {\dfrac{{{4^3}}}{3} - 0} \right] = \dfrac{{64\pi }}{3}$
So, this is the required volume of the solid of revolution.

Note: - In such types of questions the key concept we have to remember is that always remember the formula of solid of revolution around $x$-axis, and the required volume is the revolution of shaded region around $x$-axis, then simplify the integration using some basic formula which is stated above, we will get the required answer.