Question

A tree is surrounded by barriers. For each inch of the trunk diameter, the protection zone should have a radius of $ 1\dfrac{1}{3} $ feet. Find the area of the zone for the tree with a trunk circumference of $ 63 $ inches.

Answer 1

Hint: In order to find the area of the protection zone, initiate with finding the radius of the trunk using the circumference given then add with the radius of the protection zone outside the trunk to find the actual radius from the trunk. Then using the estimated radius find the area.
Formula used:
 $ Circumference = 2\pi r $
 $ 1{\text{ feet = 12 inches}} $
 $ Area = \pi {r^2} $

Complete step-by-step answer:
The rough figure using the information given:
           

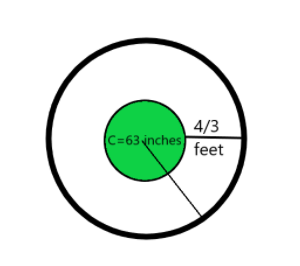
We are given a tree surrounding by barriers, where the circumference of the trunk is $ 63 $ inches, which is numerically written as:
 $ Circumference = 63 $
From the circumference formula, we know that:
 $ Circumference = 2\pi r $
Substituting the value $ Circumference = 63 $ in the above equation, we get:
 $ \Rightarrow 63 = 2\pi r $
Dividing both the sides by $ 2\pi $ :
 $ \Rightarrow \dfrac{{63}}{{2\pi }} = \dfrac{{2\pi r}}{{2\pi }} $
 $ \Rightarrow \dfrac{{63}}{{2\pi }} = r $
Substituting the value of $ \pi = \dfrac{{22}}{7} $ in the above equation:
 $ \Rightarrow \dfrac{{63}}{{2 \times \dfrac{{22}}{7}}} = r $
Solving it further, we get:
 $ \Rightarrow \dfrac{{63 \times 7}}{{2 \times 22}} = r $
 $ \Rightarrow \dfrac{{441}}{{44}} = r $
 $ \Rightarrow r = \dfrac{{441}}{{44}} \approx 10{\text{ inches}} $ …..(1)
Therefore, the radius of the trunk is $ 10{\text{ inches}} $ .
Given, the radius outside the trunk till the protection zone is $ 1\dfrac{1}{3} $ feet, which written in terms of simplest fraction as:
  $ \Rightarrow 1\dfrac{1}{3} = \dfrac{{3 \times 1 + 1}}{3} = \dfrac{{3 + 1}}{3} = \dfrac{4}{3}{\text{ feet}} $
Since, we know that:
 $ 1{\text{ feet = 12 inches}} $
 $ \Rightarrow \dfrac{4}{3}{\text{ feet = }}\dfrac{4}{3} \times {\text{12 inches}} $
 $ \Rightarrow \dfrac{4}{3} \times {\text{12 = }}\dfrac{{48}}{3} = 16{\text{ inches}} $
Therefore, the radius outside the trunk till the protection zone is:
 $ 1\dfrac{1}{3} $ feet $ = 16{\text{ inches}} $ …..(2)

Adding (1) and (2), we get:
 $ \Rightarrow \left( {10 + 16} \right){\text{ inches}} $
 $ \Rightarrow 26{\text{ inches}} $
Hence, the radius of the protection zone from the trunk is $ 26{\text{ inches}} $ .
The new figure can be made as:
 

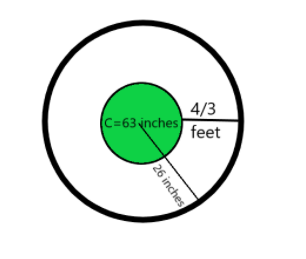
We need to find the area of the protection zone with the radius $ 26{\text{ inches}} $ .
Since, we know that Area of the circle is:
 $ Area = \pi {r^2} $
Substituting the value of radius in the above equation, we get:
 $ \Rightarrow Area = \dfrac{{22}}{7} \times {\left( {26} \right)^2}{\text{ sq}}{\text{. inches}} $
Solving it further, we get:
 $ \Rightarrow Area = \dfrac{{22}}{7} \times 676{\text{ sq}}{\text{. inches}} $
 $ \Rightarrow Area = \dfrac{{14872}}{7}{\text{ sq}}{\text{. inches}} $
 $ \Rightarrow Area = 2124.57{\text{ sq}}{\text{. inches}} $
Hence, the area for the tree with a trunk circumference of $ 63 $ inches is $ 2124.57{\text{ sq}}{\text{. inches}} $ .
So, the correct answer is “ $ 2124.57{\text{ sq}}{\text{. inches}} $ ”.

Note: It’s important to create a figure using the information given for solving easily.
Do not forget to convert the radius in feet in terms of inches as to add or subtract any two numbers it must be in the same units. It is converted using the formula $ 1{\text{ feet = 12 inches}} $ .