Question

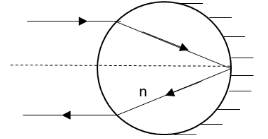
A transparent cylinder has its right half polished so as to act as a mirror. A paraxial light ray incident from the left that is parallel to the principal axis, exits parallel to the incident ray as shown. The refractive index \[n\] of the material of the cylinder is

A. 1.2
B. 1.5
C. 1.8
D. 2.0

Answer 1

Hint:Use the lens formula for the spherical surface. This formula gives the relation between the refractive index of the material of the spherical surface, refractive index of the medium in which the spherical surface is placed, distance of object from the spherical surface, distance of the image from spherical surface and radius of the spherical surface.

Formula used:
The lens formula for the spherical surface is given by
\[\dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{R}\] …… (1)
Here, \[{\mu _2}\] is the refractive index of the material of the spherical surface, \[{\mu _1}\] is the refractive index of the medium in which the spherical surface is placed, \[u\] is the distance of object from the spherical surface, \[v\] is distance of the image from spherical surface and \[R\] is radius of the spherical surface.

Complete step by step answer:
We have given that the half right side of a transparent spherical cylinder is polished so that the right half surface of the cylinder behaves as a mirror. Let \[R\] be the radius of the spherical cylinder.We have asked to calculate the refractive index of the material of the spherical cylinder.The medium in which the spherical cylinder is placed is the air medium.
The refractive index of the air medium is 1.
\[{\mu _{air}} = 1\]
The distance of the object from which the ray is incident on the mirror formed from the transparent spherical cylinder is infinity.
\[u = \infty \]
The distance at which the image of the object is formed from the transparent spherical cylinder is equal to twice the radius of the spherical cylinder.
\[v = 2R\]

Let us calculate the refractive index of the material of the spherical cylinder using equation (1). Substitute \[n\] for \[{\mu _2}\], \[{\mu _{air}}\] for \[{\mu _1}\], \[2R\] for \[v\] and \[\infty \] for \[u\] in equation (1).
\[\dfrac{n}{{2R}} - \dfrac{{{\mu _{air}}}}{\infty } = \dfrac{{n - {\mu _{air}}}}{R}\]
\[ \Rightarrow \dfrac{n}{{2R}} - 0 = \dfrac{{n - {\mu _{air}}}}{R}\]
\[ \Rightarrow \dfrac{n}{2} = n - {\mu _{air}}\]
Substitute \[1\] for \[{\mu _{air}}\] in the above equation.
\[ \Rightarrow \dfrac{n}{2} = n - 1\]
\[ \Rightarrow n - \dfrac{n}{2} = 1\]
\[ \Rightarrow \dfrac{n}{2} = 1\]
\[ \therefore n = 2\]
Therefore, the refractive index of the material of the spherical cylinder is 2.

Hence, the correct option is D.

Note: The students should be careful while substituting the values of the refractive index of the material of the spherical cylinder and refractive index of the medium in which the spherical cylinder is placed. If the values of the refractive index are substituted incorrectly, then the final answer for the refractive index of the material of the spherical cylinder will also be incorrect.