Question

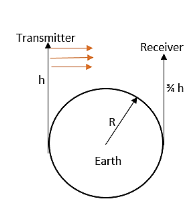
A transmitting antenna of height $h$ and the receiving antenna of height $\dfrac{3}{4}h$ are separated by a distance of $d$ for satisfactory communication in line-of-sight mode. Then, the value of $h$ is
[Given, the radius of the earth is $R$].

$\begin{align}
  & A.\dfrac{{{d}^{2}}}{2R}{{\left( 2\sqrt{2}-\sqrt{6} \right)}^{2}} \\
 & B.\dfrac{{{d}^{2}}}{4R}{{\left( 2\sqrt{2}-\sqrt{6} \right)}^{2}} \\
 & C.\dfrac{{{d}^{2}}}{R}{{\left( 2\sqrt{2}-\sqrt{6} \right)}^{2}} \\
 & D.\dfrac{{{d}^{2}}}{8R}{{\left( 2\sqrt{2}-\sqrt{6} \right)}^{2}} \\
\end{align}$

Answer 1

Hint: The height of antenna can be calculated using the equation,
${{d}_{m}}=\sqrt{2R{{h}_{T}}}+\sqrt{2R{{h}_{R}}}$
Where ${{d}_{m}}$ be the maximum distance of line of sight between the antenna and the transmitting antenna. Then after solving and rearranging we will get the value of ${{d}_{m}}$ in terms of $h$. The denominator of the term is factorized after this and then squares the both sides of the equation. This will lead you to the answer.

Complete answer:
first of all let us look at what all are given in the question.
The height of the transmitting antenna has been given as the equation,
${{h}_{T}}=h$
And also the height of the receiving antenna is given by the equation,
\[{{h}_{R}}=\dfrac{3}{4}h\]
As we know the radius of the earth is \[R\].
The maximum line of sight distance between these two antenna is given by the equation,
${{d}_{m}}=\sqrt{2R{{h}_{T}}}+\sqrt{2R{{h}_{R}}}$
In the question, it is mentioned that the value of ${{d}_{m}}$is,
\[{{d}_{m}}=d\]
Substituting all these values in it will give,

\[\begin{align}
  & d=\sqrt{2Rh}+\sqrt{2R\times \dfrac{3}{4}h} \\
 & d=\sqrt{2R}\times \left( \sqrt{h}+\sqrt{\dfrac{3h}{4}} \right) \\
\end{align}\]

Taking the \[\sqrt{2R}\] into the denominator, will give,
\[\dfrac{d}{\sqrt{2R}}=\left( \sqrt{h}+\sqrt{\dfrac{3h}{4}} \right)\]
Now let us take the common terms out,

\[\begin{align}
  & \dfrac{d}{\sqrt{2R}}=\sqrt{h}\left( 1+\sqrt{\dfrac{3}{4}} \right) \\
 & \dfrac{d}{\sqrt{2R}}=\sqrt{h}\left( \dfrac{2+\sqrt{3}}{2} \right) \\
\end{align}\]

Let us take all the terms into the left hand side keeping \[\sqrt{h}\]only in right hand side will give,
\[\dfrac{2d}{\sqrt{2R}\times \left( 2+\sqrt{3} \right)}=\sqrt{h}\]
Factoring the denominator will be given as,

\[\begin{align}
  & \sqrt{h}=\dfrac{2d\left( 2-\sqrt{3} \right)}{\sqrt{2R}} \\
 & \sqrt{h}=\dfrac{2\sqrt{2}d\left( 2-\sqrt{3} \right)}{2\sqrt{R}} \\
\end{align}\]

Cancelling the common terms in the equation,
\[\sqrt{h}=\dfrac{\sqrt{2}d\left( 2-\sqrt{3} \right)}{\sqrt{R}}\]
\[\sqrt{h}=\dfrac{d\left( 2\sqrt{2}-\sqrt{6} \right)}{\sqrt{R}}\]
Squaring the both sides of equations will give the value of height of the antenna.
\[h=\dfrac{{{d}^{2}}{{\left( 2\sqrt{2}-\sqrt{6} \right)}^{2}}}{R}\]

So, the correct answer is “Option C”.

Note:
A transmission antenna is a basic device used in radio technology. They are made up of a conductor that passes an electric current whose intensity is varying over time and converts it into radiofrequency radiation that can travel through space. A receiving antenna is having the opposite of the process done by the transmission antenna.