
A total charge of 20 $\mu C$ is divided into two parts and placed at some distance apart. If the charges experience maximum coulombic repulsion, the charges should be:
(A) $5\mu C,15\mu C$
(B) $10\mu C,10\mu C$
(C) $12\mu C,8\mu C$
(D) $\dfrac{40}{3}\mu C,\dfrac{20}{3}\mu C$
Answer
558.9k+ views
Hint: Consider the divided charges as q and $(20-q)$ places at some distance apart. To calculate the maximum coulombic repulsion between the charges, we equate the differentiation of Coulomb force with respect to charge to zero and then calculate the value of charge q.
Complete step by step answer:
According to the question, a total charge of 20 $\mu C$ is divided into two parts and placed at some distance apart, say R.
Let us consider the two charges as q and $(20-q)$as shown in the figure below.
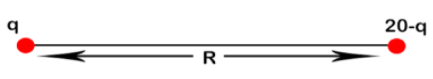
The two charges are of the same magnitude so they repel each other and the formula for coulomb repulsion is given by,
$F=\dfrac{1}{4\pi {{\in }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{R}^{2}}}$ ….(i)
Here,
${{q}_{1}}=q$ and ${{q}_{2}}=20-q$
So, putting the above values in equation (i) we get,
$F=\dfrac{1}{4\pi {{\in }_{0}}}\dfrac{q(20-q)}{{{R}^{2}}}$ ….(ii)
Now, for the maximum coulombic repulsion between the charges q and $(20-q)$, we differentiate the Coulomb force F with respect to charge q, we get,
$\dfrac{dF}{dq}=\dfrac{1}{4\pi {{\in }_{0}}{{R}^{2}}}\dfrac{d}{dq}[q(20-q)]$
$\Rightarrow \dfrac{dF}{dq}=\dfrac{1}{4\pi {{\in }_{0}}{{R}^{2}}}\dfrac{d}{dq}[20q-{{q}^{2}})]$
$\Rightarrow \dfrac{dF}{dq}=\dfrac{20-2q}{4\pi {{\in }_{0}}{{R}^{2}}}$ ….(iii)
Now for calculating the value of q we equate the maximum coulombic repulsion between the charges q and $(20-q)$ i.e. equation (iii) to zero.
$\dfrac{dF}{dq}=0$
$\Rightarrow \dfrac{20-2q}{4\pi {{\in }_{0}}{{R}^{2}}}=0$
$\Rightarrow 20-2q=0$
$\Rightarrow q=10\mu C$
Also,
$\Rightarrow 20-q=(20-10)\mu C=10\mu C$
Hence, the two charges experience maximum coulombic repulsion when they are divided in equal parts i.e. 10$\mu C$ and 10$\mu C$.
Therefore, the correct answer is option (B).
Additional Information:
The formula for coulomb force is given by,
$F=k\dfrac{{{q}_{1}}{{q}_{2}}}{{{R}^{2}}}$
Where, $k=\dfrac{1}{4\pi {{\in }_{0}}}$is the Coulomb constant, also called the electric force constant in electrostatics is,
$k=8.9875517923\times {{10}^{9}}kg\cdot {{m}^{3}}\cdot {{s}^{-2}}\cdot {{C}^{-2}}$
And
${{\in }_{0}}=8.8541878128\times {{10}^{-12}}F\cdot {{m}^{-1}}$ is the permittivity of free space or vacuum.
Note:
For solving such questions students should memorize the formula for Coulomb force between two charges placed some distance apart. Also the concept of calculating maximum force experienced by equating the derivative to zero should be remembered.
Complete step by step answer:
According to the question, a total charge of 20 $\mu C$ is divided into two parts and placed at some distance apart, say R.
Let us consider the two charges as q and $(20-q)$as shown in the figure below.
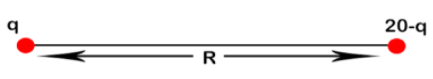
The two charges are of the same magnitude so they repel each other and the formula for coulomb repulsion is given by,
$F=\dfrac{1}{4\pi {{\in }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{R}^{2}}}$ ….(i)
Here,
${{q}_{1}}=q$ and ${{q}_{2}}=20-q$
So, putting the above values in equation (i) we get,
$F=\dfrac{1}{4\pi {{\in }_{0}}}\dfrac{q(20-q)}{{{R}^{2}}}$ ….(ii)
Now, for the maximum coulombic repulsion between the charges q and $(20-q)$, we differentiate the Coulomb force F with respect to charge q, we get,
$\dfrac{dF}{dq}=\dfrac{1}{4\pi {{\in }_{0}}{{R}^{2}}}\dfrac{d}{dq}[q(20-q)]$
$\Rightarrow \dfrac{dF}{dq}=\dfrac{1}{4\pi {{\in }_{0}}{{R}^{2}}}\dfrac{d}{dq}[20q-{{q}^{2}})]$
$\Rightarrow \dfrac{dF}{dq}=\dfrac{20-2q}{4\pi {{\in }_{0}}{{R}^{2}}}$ ….(iii)
Now for calculating the value of q we equate the maximum coulombic repulsion between the charges q and $(20-q)$ i.e. equation (iii) to zero.
$\dfrac{dF}{dq}=0$
$\Rightarrow \dfrac{20-2q}{4\pi {{\in }_{0}}{{R}^{2}}}=0$
$\Rightarrow 20-2q=0$
$\Rightarrow q=10\mu C$
Also,
$\Rightarrow 20-q=(20-10)\mu C=10\mu C$
Hence, the two charges experience maximum coulombic repulsion when they are divided in equal parts i.e. 10$\mu C$ and 10$\mu C$.
Therefore, the correct answer is option (B).
Additional Information:
The formula for coulomb force is given by,
$F=k\dfrac{{{q}_{1}}{{q}_{2}}}{{{R}^{2}}}$
Where, $k=\dfrac{1}{4\pi {{\in }_{0}}}$is the Coulomb constant, also called the electric force constant in electrostatics is,
$k=8.9875517923\times {{10}^{9}}kg\cdot {{m}^{3}}\cdot {{s}^{-2}}\cdot {{C}^{-2}}$
And
${{\in }_{0}}=8.8541878128\times {{10}^{-12}}F\cdot {{m}^{-1}}$ is the permittivity of free space or vacuum.
Note:
For solving such questions students should memorize the formula for Coulomb force between two charges placed some distance apart. Also the concept of calculating maximum force experienced by equating the derivative to zero should be remembered.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




