Question

A took 15 seconds to cross a rectangular field diagonally walking at a rate of $52\,m/\min $and B took the same time to cross the same field along its sides, walking at the rate of $68\,m/\min $. The area of the field is:
A. $30\,{{m}^{2}}$
B. $40\,{{m}^{2}}$
C. $50\,{{m}^{2}}$
D. $60\,{{m}^{2}}$

Answer 1

Hint: A crosses the rectangular field diagonally means it travels along the diagonal, and B crosses along its side means it travels along the boundary line of the rectangle. The area of the rectangle is calculated by length x breadth. Rate is the speed at which A and B are travelling . Here, the area of the field is the area of the rectangle.

Complete step by step solution:.

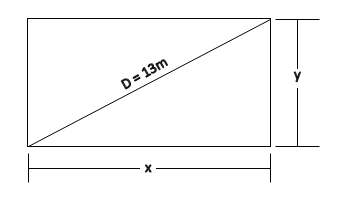
Step 1: Rate of A=$52\,m/\min $ =$\dfrac{52}{60}\,m/\sec $=$\dfrac{13}{15}\,m/\sec $
      Rate of B=$68\,m/\min $ =$\dfrac{68}{60}\,m/\sec $ =$\dfrac{17}{15}\,\,m/\sec $
Step 2: Distance travelled by A= $Rate\,of\,A\,\times \,\,time\,taken$=$\dfrac{13}{15}\,\times 15$ =$13\,m$
     Distance travelled by B= $Rate\,of\,B\,\times \,time\,taken$=$\dfrac{17}{15}\,\times 15$ =$17\,m$
Step 3: Since B crosses the field along its sides therefore, it is basically sum of two sides of rectangle i.e
     $x+y=17$
     Squaring both sides we get,
     \[\begin{align}
& \\
& {{(x+y)}^{2}}={{(17)}^{2}} \\
& {{x}^{2}}+{{y}^{2}}+2xy={{(17)}^{2}} \\
& {{(D)}^{2}}+2xy={{(17)}^{2}}\,\,\,[\because {{x}^{2}}+{{y}^{2}}={{D}^{2}}]\, \\
&2xy={{(17)}^{2}}\,-{{(D)}^{2}} \\
&2xy={{(17)}^{2}}\,-{{(13)}^{2}}\,\,\,\,\,\,[\because D\,is\,dis\tan ce\,traveled\,by\,A]\,\,\, \\
&2xy=289-169 \\
&2xy=120 \\
&xy=60{{m}^{2}} \\
& \\
& \, \\
\end{align}\]
∴$xy$ is the area of the rectangular field. It comes out to be $60\,{{m}^{2}}$

Note: In this type of questions students often get confused while determining the path. Do not make this mistake and don’t forget to use the Pythagoras theorem.