Question

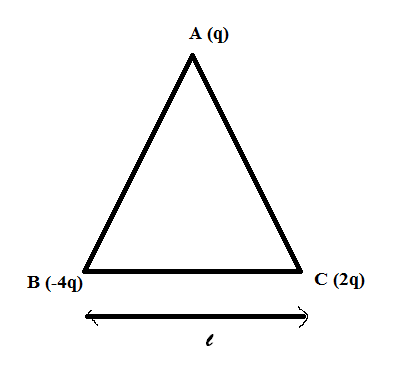
(a) Three point charges q, -4q and 2q are placed at the vertices of an equilateral triangle ABC of side ‘l’ as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of work done to separate the charges at infinite distance.

Answer 1

Hint: The magnitude of coulombic force due to a charge Q on another charge q is given by $\dfrac{KQq}{{{r}^{2}}}$ where K is the universal electric constant = $9\times {{10}^{9}}kg.{{m}^{3}}{{s}^{-4}}{{A}^{-2}}$ and r is the linear distance between them. Two unlike charges have attractive force while like charges have repulsive force.
The amount of work done to separate a system of charges to infinite distance is the negative of the electric potential energy of the system.
Complete step by step answer:
A) The magnitude of Coulombic force due to a charge Q on another charge q is given by $\dfrac{KQq}{{{r}^{2}}}$ where K is the universal electric constant = $9\times {{10}^{9}}kg.{{m}^{3}}{{s}^{-4}}{{A}^{-2}}$ and r is the linear distance between them. Two unlike charges have attractive force while like charges have repulsive force.
Therefore, the magnitude of force on A due to B is
${{F}_{2}}=\dfrac{Kq\times 4q}{{{l}^{2}}}=\dfrac{4K{{q}^{2}}}{{{l}^{2}}}$
 Along AB and towards B, since they are unlike charges and attract each other.
The magnitude of force on A due to C is
 ${{F}_{1}}=\dfrac{Kq\times 2q}{{{l}^{2}}}=\dfrac{2K{{q}^{2}}}{{{l}^{2}}}$
Along AC and away from C, since they are like charges and repel each other.

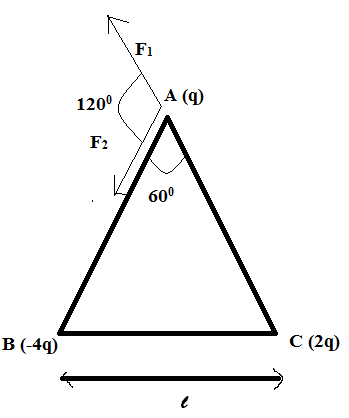
Now, the cosine law of vectors states that the resultant magnitude of two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ is given by $\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }$ where A and B are the magnitudes and $\theta $ is the angle between the two vectors.
Therefore, the resultant force magnitude on charge q is $\sqrt{{{F}_{1}}^{2}+{{F}_{2}}^{2}+2{{F}_{1}}{{F}_{2}}\cos \theta }$ . The angle between them as shown in the above figure is ${{120}^{0}}$
$=\sqrt{{{\left( \dfrac{4K{{q}^{2}}}{{{l}^{2}}} \right)}^{2}}+{{\left( \dfrac{2K{{q}^{2}}}{{{l}^{2}}} \right)}^{2}}+\left( 2\times \dfrac{4K{{q}^{2}}}{{{l}^{2}}}\times \dfrac{2K{{q}^{2}}}{{{l}^{2}}} \right)\cos {{120}^{0}}}$
=$\sqrt{\left( \dfrac{16{{K}^{2}}{{q}^{4}}}{{{l}^{4}}} \right)+\left( \dfrac{4{{K}^{2}}{{q}^{4}}}{{{l}^{4}}} \right)+\left( 2\times \dfrac{8{{K}^{2}}{{q}^{4}}}{{{l}^{4}}} \right)\times \left( -0.5 \right)}$ $=\sqrt{\left( \dfrac{12{{K}^{2}}{{q}^{4}}}{{{l}^{4}}} \right)}=\dfrac{2\sqrt{3}K{{q}^{2}}}{{{l}^{2}}}$ $\left( \because \cos {{120}^{0}}=-0.5 \right)$
Hence, the magnitude of the resultant force on the charge q is$\dfrac{2\sqrt{3}K{{q}^{2}}}{{{l}^{2}}}$ where K is the universal electric constant = $9\times {{10}^{9}}kg.{{m}^{3}}{{s}^{-4}}{{A}^{-2}}$.
B) The amount of work required to separate the charges to infinite distance is the negative of the magnitude of the total electric potential of the system. The potential of the system is the sum of the electric potential of each charge.
The electric potential of a charge in the presence of another charge Q is given by $\dfrac{KQ}{r}$ where the value is negative if the charges are unlike and positive if they are like.
Thus, the electric potential of charge q due to other two charges is given by
$\dfrac{-4Kq}{l}+\dfrac{+2Kq}{l}=\dfrac{-2Kq}{l}$ ---(1)
Thus, the electric potential of charge -4q due to other two charges is given by
$\dfrac{-Kq}{l}+\dfrac{-2Kq}{l}=\dfrac{-3Kq}{l}$ ---(2)
Thus, the electric potential of charge 2q due to other two charges is given by
$\dfrac{-4Kq}{l}+\dfrac{Kq}{l}=\dfrac{-3Kq}{l}$ ---(3)
Therefore, the total electric potential of the system is just the sum of (1), (2) and (3) =$\dfrac{-2Kq}{l}+\dfrac{-3Kq}{l}+\dfrac{-3Kq}{l}=\dfrac{-8Kq}{l}$
Therefore, the amount of work required to dismantle this system, that is separate the charges to infinity, is the negative of this value, that is $\dfrac{8Kq}{l}$.
Note: The electric potential of the system can also be found out by considering that the system was formed by bringing the charges one by one from infinity and calculating the work required in doing so and after summing up considering the negative of the magnitude. Thus, in this way for the first charge no work is required as there are no charges in the system presently. While bringing the second charge, the first charge will be present and cause a change in electric potential and while bringing the third charge, the other two charges present will cause a drop in potential.
Any charge can be considered to be brought first and the answer will remain the same. The answers by this method and the one elaborated in the answer section must match. This is also a good way of verification if your answer is correct.