Question

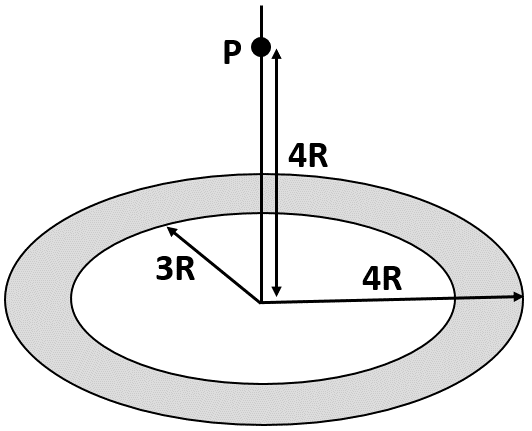
A thin uniform annular disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass from point P on its axis to infinity is,

$\begin{align}
  & A)\dfrac{2GM}{7R}\left( 4\sqrt{2}-5 \right) \\
 & B)-\dfrac{2GM}{7R}\left( 4\sqrt{2}-5 \right) \\
 & C)\dfrac{GM}{4R} \\
 & D)\dfrac{2GM}{5R}\left( \sqrt{2}-1 \right) \\
\end{align}$

Answer 1

Hint: We must know that to bring a unit mass from point P to infinity, work has to be done against the gravitational field of the disc. So, we will find the gravitational potential of a small element of thickness $dr$. Then by finding the potential at P due to this small element and integrating it from the limit of inner radius to outer, we can find the work required to take a unit mass from point P to infinity.

Complete step-by-step Solution:
Let us consider that the work needed to take a unit mass from point P to $\infty $ is $-{{V}_{p}}$ where, ${{V}_{p}}$ is the gravitational potential due to the disc. For finding ${{V}_{p}}$, we will consider a small element of thickness $dr$ from the disc .

Now, let us take such an element at distance r from the center of the disc as shown in the figure.

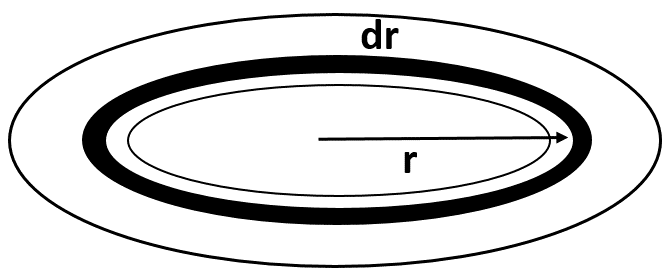
Now, the mass of the small element is given by,
$dm=\dfrac{M(2\pi rdr)}{\pi {{(4R)}^{2}}-\pi {{(3R)}^{2}}}=\dfrac{2Mrdr}{7{{R}^{2}}}$

So, the gravitational potential due to the entire disc is given by integrating the potential due to the number of these small elements within the limit 3R to 4R. That is,
\[{{V}_{p}}=-\int_{3R}^{4R}{\dfrac{Gdm}{\sqrt{{{r}^{2}}+16{{R}^{2}}}}}\]

Here, the distance of a small element from P is found using Pythagoras theorem.

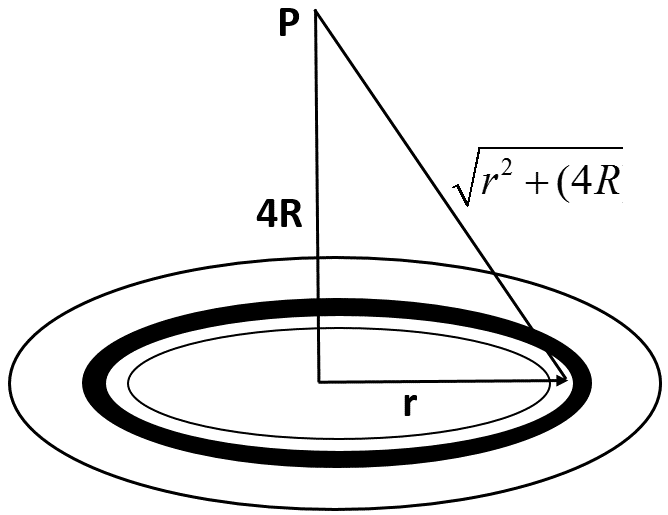
Now, substituting $dm$ in the above equation,
\[\Rightarrow {{V}_{p}}=-\int_{3R}^{4R}{\dfrac{2MGrdr}{7{{R}^{2}}\sqrt{{{r}^{2}}+16{{R}^{2}}}}}=-\dfrac{2MG}{7{{R}^{2}}}\int_{3R}^{4R}{\dfrac{rdr}{\sqrt{{{r}^{2}}+16{{R}^{2}}}}}\]
Let us assume \[\sqrt{{{r}^{2}}+16{{R}^{2}}}\] as ${{x}^{2}}$. That is,
\[\sqrt{{{r}^{2}}+16{{R}^{2}}}={{x}^{2}}\]

Differentiating both sides, we will get
\[\begin{align}
  & 2rdr=2xdx \\
 & \Rightarrow rdr=xdx \\
\end{align}\]
Now, when r=3R, \[x=\sqrt{9{{R}^{2}}+16{{R}^{2}}}=5R\]
Now, when r=4R, \[x=\sqrt{16{{R}^{2}}+16{{R}^{2}}}=4\sqrt{2}R\]

So, our limits will be changing according to this.
\[\begin{align}
  & \Rightarrow {{V}_{p}}=-\dfrac{2MG}{7{{R}^{2}}}\int_{5R}^{4\sqrt{2}R}{\dfrac{xdx}{\sqrt{{{r}^{2}}+16{{R}^{2}}}}} \\
 & \Rightarrow {{V}_{p}}=-\dfrac{2MG}{7{{R}^{2}}}\int_{5R}^{4\sqrt{2}R}{dx}=-\dfrac{2MG}{7{{R}^{2}}}\left[ x \right]_{5R}^{4\sqrt{2}R} \\
 & \therefore {{V}_{p}}=-\dfrac{2MG}{7{{R}^{2}}}\left( 4\sqrt{2}R-5R \right) \\
\end{align}\]
Or we can write this as, \[{{V}_{p}}=-\dfrac{2MG}{7R}\left( 4\sqrt{2}-5 \right)\]

Therefore the work required to take a unit mass from point P to infinity is found to be \[{{V}_{p}}=-\dfrac{2MG}{7R}\left( 4\sqrt{2}-5 \right)\].

So, the option B is correct.

Note:
The key element of this type of questions is understanding that the work needed to be done will be equal to the potential of the system. The negative sign will be there as work needed to be done against the potential. Also, the tricky part is changing the limits of the integration to our desired variable. So, we must be very careful while doing it.