Question

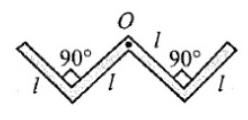
A thin rod of length $4l$ , mass $4m$ is bent at the points as shown in figure. What is the moment of inertia of the road about the axis passing point O and perpendicular to the plane of the paper.
                                                      

A.$\dfrac{M{{l}^{2}}}{3}$
B.$\dfrac{10M{{l}^{2}}}{3}$
C.$\dfrac{M{{l}^{2}}}{12}$
D.$\dfrac{M{{l}^{2}}}{24}$

Answer 1

Hint:Relation between the moment of inertia and mass
$I=m{{r}^{2}}$
Where $m=$ is the mass
And $I=$ moment of inertia

Complete step by step answer:
First, we know about the moment of inertia
Moment of inertia:- Moment of inertia is defined as the product of the mass of section and the square of the distance between the reference axis and the centroid of the section.
It is defined as $I$.
 $I=m{{r}^{2}}$
Or
Moment of inertia $I$ is defined as the ratio of the net angular momentum of a system to its angular velocity around a principal axis. That is
$I=\dfrac{L}{\omega }$
Where $I=$ Moment of inertia
$L=$ Angular momentum of a system
$\omega =$ Angular velocity
Since the length of the rod is $4l$ and mass $4m$
Length of AB=BO=OC=CD=$l$
Mass=$m$ (for all length part)
                                                     

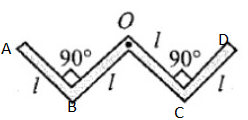
Moment of inertia of a rod about to end $=\dfrac{m{{l}^{2}}}{3}$
Moment of inertia of AB, BO, OC, CD about B, D, C respectively $=\dfrac{m{{l}^{2}}}{3}$
From parallel axis theorem,
Moment of inertia of AB about O
$=\dfrac{m{{l}^{2}}}{3}+m{{l}^{2}}$
$=\dfrac{4m{{l}^{2}}}{3}$
Similarly on CD about O,
$=\dfrac{4m{{l}^{2}}}{3}$
So moment of inertia of rod about O
$I=\dfrac{m{{l}^{2}}}{3}+\dfrac{m{{l}^{2}}}{3}+\dfrac{4m{{l}^{2}}}{3}+\dfrac{4m{{l}^{2}}}{3}$
$I=\dfrac{10m{{l}^{2}}}{3}$

Note:
Student takes the same formula for both sidewise rotation and around the centre but the formula for both are different.