Question

A thin Plano-convex lens acts like a concave mirror of focal length $0.2m$ when silvered from its plane surface. The refractive index of the material of the lens is $1.5$. The radius of curvature of the convex surface of the lens will be:
$\begin{align}
  & \text{A}\text{. }0.1m \\
 & \text{B}\text{. }0.75m \\
 & \text{C}\text{. }0.4m \\
 & \text{D}\text{. }0.2m \\
\end{align}$

Answer 1

Hint: In a Plano-convex lens, one surface is curved outwards, that is, the convex surface, and the other surface is flat. The focal length of a Plano-convex lens can be determined using lens maker formula. The focal length of a plane or flat surface is infinity.

Formula used:
Lens maker formula:
$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$

Complete step by step answer:
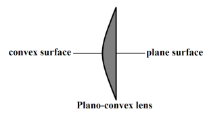
Plano-convex lens is a type of lens that is plane on one side and convex on the other. Plano-convex lenses have one positive convex face and a flat or plane face on the opposite side of the lens. These lens elements focus parallel light rays into a focal point that is positive and forms a real image that can be projected on a screen or manipulated by spatial filters.

We are given that a thin Plano-convex lens acts like a concave mirror of focal length $0.2m$ when it is silvered from its plane surface,
Focal length Plano-convex lens, $f=0.2m=20cm$
Refractive index of material of lens (behaving like concave mirror), $\mu =1.5$
Using combinational lens formula, we have,

$\dfrac{1}{{{f}_{1}}}=\dfrac{2}{f}+\dfrac{1}{{{f}_{m}}}$
Where,
${{f}_{1}}$is the focal length of combination, that is, Plano-convex lens
$f$ is the focal length of convex surface of lens
${{f}_{m}}$ is the focal length of mirror surface

We have,
${{f}_{m}}=\infty $, because focal length of plane surface is infinite
$\dfrac{1}{{{f}_{1}}}=\dfrac{2}{f}+\dfrac{1}{{{f}_{m}}}$
Putting values of${{f}_{1}}$and ${{f}_{m}}$

$\begin{align}
  & \dfrac{1}{{{f}_{1}}}=\dfrac{2}{f} \\
 & f=2{{f}_{1}} \\
 & f=2\times 20=40cm \\
\end{align}$

Using lens maker formula,

$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
Putting values,
$\begin{align}
  & f=40cm \\
 & \mu =1.5 \\
 & {{R}_{2}}=\infty \\
\end{align}$

We get,

$\begin{align}
  & \dfrac{1}{40}=\left( 1.5-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{\infty } \right) \\
 & \dfrac{1}{40}=\dfrac{1}{2{{R}_{1}}} \\
 & {{R}_{1}}=20cm \\
\end{align}$
The radius of curvature of the convex surface of the lens is $20cm$ or $0.2m$
Hence, the correct option is D.

Note:
A Plano-convex lens is a combination of two different types of surfaces, one flat and the other one being curved outwards. The focal length of a plane surface is always infinity. It can be assumed as a spherical surface of infinite radius of curvature. Since the radius of curvature of the plane surface is infinity, thus its focal length is also infinity. The focal length of a Plano-convex lens is determined using lens maker formula.