Question

A thin glass (refractive index 1.5) lens has optical power of -5D in air. Its optical power in a liquid medium with refractive index 1.6 will be:
A. -1D
B. 1D
C. -0.625D
D. 0.625D

Answer 1

Hint: Firstly recall the expression for power in terms of focal length. Now we have the lens maker’s formula which expresses the reciprocal of focal length in terms of refractive indices and radius of curvature. Now you could find the ratio of the power of the lens in air to that in the medium, doing so the radius terms gets cancelled and gets an expression in terms of refractive indices which is directly given in the question and by substituting them we get the answer.

Formula used:
Expression for power of lens,
$P=\dfrac{1}{f}$
Lens maker’s formula,
$\dfrac{1}{f}=\left( \dfrac{{{n}_{2}}}{{{n}_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$

Complete step by step answer:
We are given a thin glass prism of refractive index 1.5 with optical power of -5D in air. We are asked to find the optical power of the lens in a liquid medium with refractive index 1.6.
 We know that power is the degree of convergence or divergence introduced by the lens in the light falling on it. It is also defined as the tangent of the angle by which the beam of light at a unit distant from the optical centre is converge or diverge.

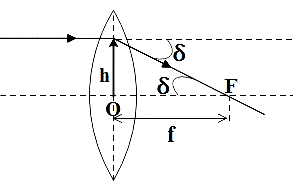
$\tan \delta =\dfrac{h}{f}$
For h=1,
$\tan \delta =\dfrac{1}{f}$
For very small δ,
$\delta =\dfrac{1}{f}$
$\Rightarrow P=\dfrac{1}{f}$ ………………………… (1)
SI unit for power of a lens is dioptre (D).
Now let us recall the lens maker’s formula which is given by,
$\dfrac{1}{f}=\left( \dfrac{{{n}_{2}}}{{{n}_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$ …………………………….. (2)
Where,
f = focal length of the lens
${{n}_{1}}$ = refractive index of the medium from which the light is incident
${{n}_{2}}$ = refractive index of the lens
${{R}_{1}}$ = radius of curvature of the lens on one side
${{R}_{2}}$ = radius of curvature of the lens on other side
 Also, from (1) and (2), we have,
$P=\left( \dfrac{{{n}_{2}}}{{{n}_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
In the question, we have two cases, first when the lens is kept in air $\left( {{n}_{a}} \right)$and second when the lens is kept in a medium of refractive index 1.6.
In air the power is given by,
${{P}_{a}}=\left( \dfrac{{{n}_{g}}}{{{n}_{a}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
$\Rightarrow {{P}_{a}}=\left( \dfrac{1.5}{1}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$ …………………………… (3)
In the other medium the power is given by,
${{P}_{m}}=\left( \dfrac{{{n}_{m}}}{{{n}_{g}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
$\Rightarrow {{P}_{m}}=\left( \dfrac{1.5}{1.6}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$ …………………………… (4)
Dividing (4) by (3) gives,
$\dfrac{{{P}_{m}}}{{{P}_{a}}}=\dfrac{\left( \dfrac{1.5}{1.6}-1 \right)}{\left( \dfrac{1.5}{1}-1 \right)}$
$\dfrac{{{P}_{m}}}{{{P}_{a}}}=\dfrac{-0.0625}{0.5}$
But ${{P}_{a}}$ is given as -5D,
${{P}_{m}}=-0.125\times -5$
${{P}_{m}}=0.625D$
Therefore, the optical power of the given lens in a liquid medium with refractive index 1.6 is 0.625D.

So, the correct answer is “Option D”.

Note: In the question we are given the values for refractive indices and power of lens in air, but we don't have any expression that directly relates the two. So we derive the required formulae by combining two separate formulas that we know. Also, in equation (1) the focal length should be in meters for us to get the power in dioptre.