
A thin film of thickness t and index of refraction
Answer
506.4k+ views
1 likes
Hint: The thin-film interference method or occurrence when a light wave is reflected off from the two surfaces with the surface separation is that of the wavelength distance. Due to this occurrence, the phase differences between the two surfaces are negligible when light passes from denser to rarer. Hence, the path difference for constructive interference of transmission of light is given as:
where
Complete step by step solution:
Let us draw the diagram to show how the light ray when traveling from rarer to denser medium refracts and from denser to rarer reflects from surface 1 to 2 and from 2 to 1.
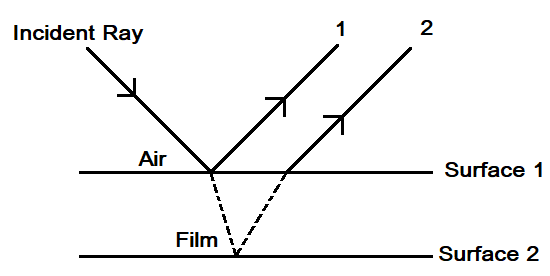
Hence, there are two types of transmission of light i.e. constructive and destructive. For constructive transmission, the phase difference between the travelling of light is 180 degrees. The light from the incident ray is reflected and refracted from the first surface and second surface simultaneously. Hence, the minimum thickness for the transmission of light from surface 1 to surface 2 is:
Placing the value of
Note:There are two constructive Interference for reflection and transmission are given as:
For constructive Interference for reflection is:
For constructive Interference for transmission is:
And the value of the wavelength transmission is
where
Complete step by step solution:
Let us draw the diagram to show how the light ray when traveling from rarer to denser medium refracts and from denser to rarer reflects from surface 1 to 2 and from 2 to 1.

Hence, there are two types of transmission of light i.e. constructive and destructive. For constructive transmission, the phase difference between the travelling of light is 180 degrees. The light from the incident ray is reflected and refracted from the first surface and second surface simultaneously. Hence, the minimum thickness for the transmission of light from surface 1 to surface 2 is:
Placing the value of
Note:There are two constructive Interference for reflection and transmission are given as:
For constructive Interference for reflection is:
For constructive Interference for transmission is:
And the value of the wavelength transmission is
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Trending doubts
Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Which are the Top 10 Largest Countries of the World?

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Derive an expression for electric potential at point class 12 physics CBSE




