Question

A thin convex lens of focal length 'f' is put on a plane mirror as shown in the figure. When an object is kept at a distance 'a' from the lens - mirror combination, its image is formed at a distance $\dfrac{a}{3}$ in front of the combination. The value of 'a' is:-

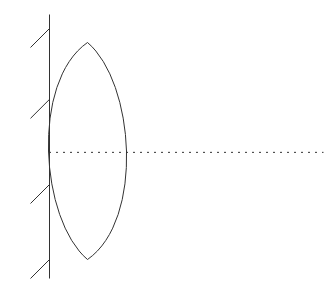
A. 2f
B. $\dfrac{3}{2}f$
C. 3f
D. f

Answer 1

Hint: Lens are the things which will allow the light to pass through them with convergence or divergence. Depending on whether the lens will converge or diverge the rays they are divided into convex and concave lenses. Their capacity of convergence or divergence is given by power of the lens. When the mirror is nearly attached to the lens the power will be doubled. Based on this we will solve the problem.

Formula used:
$\eqalign{
  & P = {P_1} + {P_2} \cr
  & P = \dfrac{1}{f} \cr} $

Complete step by step answer:
The main difference between the lens and mirrors is there are many ways to change the effective focal length of a lens without varying them geometrically. For example if we put the lens in a different medium from air then the refractive index in that medium will be different from that of air. This is not possible for mirrors. They have constant focal length and don’t vary with the medium.
This is because the rays will suffer refraction in the lens and that refraction depends upon the surrounding medium and the entering medium. In case of mirrors there will be no refraction hence the focal length of the mirror won’t change.
Power of the lens is given by the inverse of the focal length. When two lenses are brought very close to each other then their powers will add up and focal length will vary and we get effective focal length of the new lens.
Similarly if we bring a plain mirror very near to the lens then the rays first refraction occurs then reflection from mirror occurs then again refraction occurs. Hence refraction occurs twice. So power will double.

$\eqalign{
  & P = \dfrac{1}{f} \cr
  & \Rightarrow \left| P \right| = {P_1} + {P_2} \cr
  & \Rightarrow \left| P \right| = \dfrac{1}{f} + \dfrac{1}{f} \cr
  & \therefore \left| P \right| = \dfrac{2}{f} \cr} $
Since there is reflection happening the power will have negative signs as rays get reflected. So
$\eqalign{
  & P = - \dfrac{2}{f} \cr
  & \Rightarrow {f_{eff}} = \dfrac{{ - f}}{2} \cr} $
This entire system acts as a concave mirror with focal length -f/2
Apply mirror equation to get value of ‘a’
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Where ‘u’ is object distance and ‘v’ is the image distance
Since objects and images are formed on the same side they will have negative signs.
$\eqalign{
  & \dfrac{1}{{\left( {\dfrac{{ - a}}{3}} \right)}} + \dfrac{1}{{ - a}} = \dfrac{1}{{\left( {\dfrac{{ - f}}{2}} \right)}} \cr
  & \Rightarrow \dfrac{{ - 3}}{a} + \dfrac{{ - 1}}{a} = \dfrac{{ - 2}}{f} \cr
  & \therefore a = 2f \cr} $
Hence option A will be the correct answer.

Note: Here the system is entirely changed into a concave mirror. The lens refractive index can be varied in such a way that a convex lens can behave as the concave lens without any change in shape. This is when we place the lens in the medium of refractive index greater than the lens refractive index, then the convex lens would change into concave while the concave lens would change into convex.