Question

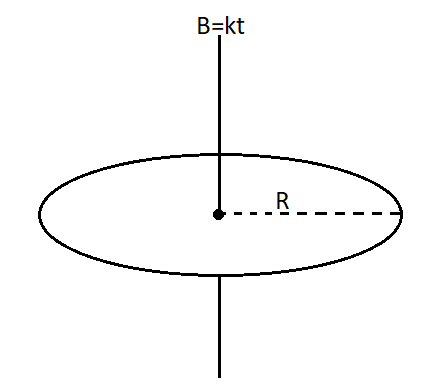
A thin conducting horizontal disc of mass $m$ having total charge $q$ distributed uniformly over its surface can rotate freely about its own axis. Initially when the disc $B$ stationary a magnetic field is directed perpendicular to the plane is switched on at $t = 0$. Find the angular velocity $\omega $ acquired by disc as a function of time, if $B = kt$, where $t$ is time.

Answer 1

Hint
We need to find the electric field that is induced due to the time varying magnetic field. Then we can calculate the force due to that electric field. We can then find the torque due to that force and equate that to the product of the moment of inertia and linear acceleration. The angular acceleration can be calculated from the linear acceleration.
Formula Used: In this solution we will be using the following formula,
$\oint {E \cdot dl} = - \dfrac{d}{{dt}}\int {B \cdot dA} $
Where $E$ is the electric field and $B$ is the magnetic field.
$F = qE$ where $F$ is the force on charge $q$ due to the electric field.
$\tau = \int {rdF} $ where $\tau $ is the torque.
and $\tau = I\alpha $ where $I$ is the moment of inertia of the disc and $\alpha $ is the angular acceleration.

Complete step by step answer
Let us consider a small ring inside the disc of radius $r$.We need to first find the electric field that is induced in the ring due to the rotating charged disc in the time varying magnetic field. It is given by the formula,
$\oint {E \cdot dl} = - \dfrac{d}{{dt}}\int {B \cdot dA} $
Now since the electric field and the magnetic field are uniform on the surface of the disc, they come out of the integration. And the closed surface integration over the disc will give $2\pi r$ where $r$the radius of a smaller circle inside the disc is and the integration over the area will give, $\pi {r^2}$
So substituting the values we get,
$E \times 2\pi r = - \pi {r^2}\dfrac{d}{{dt}}\left( B \right)$
We can substitute the value of the magnetic field as, $B = kt$ and cancel the $\pi r$ on both sides of the equation to get,
$E \times 2 = - r\dfrac{d}{{dt}}\left( {kt} \right)$
On doing the differentiation we get the value of the electric field as,
$E = - \dfrac{{rk}}{2}$
Let the charge on the small ring be $dq$. So the force experienced by the charged ring in the electric field is given by $dF = \left( {dq} \right)E$
Now the charge on the ring can be given by,
$dq = \dfrac{q}{{\pi {R^2}}} \times 2\pi rdr$
So substituting the value of charge and electric field we get force as,
$dF = \dfrac{q}{{\pi {R^2}}} \times 2\pi rdr \times \dfrac{{rk}}{2}$
We neglected the negative sign as we only considered the magnitude.
Therefore, the total torque due to the whole disc is,
$\tau = \int {rdF} $
Substituting the values,
$\tau = \int {\left( {r\dfrac{q}{{\pi {R^2}}} \times 2\pi rdr \times \dfrac{{rk}}{2}} \right)} $
We can set the limit from 0 to $R$
Taking the constants out of integration we get,
$\tau = \dfrac{q}{{\pi {R^2}}} \times 2\pi \times \dfrac{k}{2}\int_0^R {{r^3}dr} $
Now cancelling all the common terms among the constants, and doing the integration we get,
$\tau = \dfrac{q}{{{R^2}}} \times k \times \left. {\dfrac{{{r^4}}}{4}} \right|_0^R$
Substituting the limits,
$\tau = \dfrac{q}{{{R^2}}} \times k \times \dfrac{{{R^4}}}{4}$
On cancelling ${R^2}$ from numerator and denominator we get,
$\tau = \dfrac{{kq{R^2}}}{4}$
This torque is also given by the product of the moment of inertia and angular acceleration. That is,
$\tau = I\alpha $
From here we can find linear acceleration as,
$\alpha = \dfrac{\tau }{I}$
The moment of inertia of the disc is given by, $I = \dfrac{{m{R^2}}}{2}$
Hence we get angular acceleration as,
$\alpha = \dfrac{{\dfrac{{kq{R^2}}}{4}}}{{\dfrac{{m{R^2}}}{2}}}$
On simplifying we get
$\alpha = \dfrac{{kq{R^2}}}{4} \times \dfrac{2}{{m{R^2}}}$
Cancelling the like terms,
$\alpha = \dfrac{{kq}}{{2m}}$
The angular speed will be given by just multiplying the angular acceleration with time as,
$\omega = \dfrac{{kq}}{{2m}} \times t$
So the angular acceleration is $\omega = \dfrac{{kqt}}{{2m}}$.

Note
The moment of inertia of any body is its tendency to resist angular acceleration. It is given by the sum of the products of the masses and the square of the distance of the particles from the axis of rotation. For a circular disc, the moment of inertia about the center of mass can be calculated as, $I = \dfrac{{m{R^2}}}{2}$.