Question

A thick rope of density \[\rho \]and length L is hung from a rigid support. The increase in the length of the rope due to its own weight is (Y is Young’s modulus)
A) $\dfrac{{0.1}}{{4Y}}\rho {L^2}g$
B) $\dfrac{1}{{2Y}}\rho {L^2}g$
C) $\dfrac{{\rho {L^2}g}}{Y}$
D) $\dfrac{{\rho Lg}}{Y}$

Answer 1

Hint: Take a small element of rope length at a certain distance from the top, force applied here is only due to the weight of the rope. Use the stress-strain equation and integrate it to find the relation of increase in its length due to its own weight.

Complete step by step answer:
Step1: Consider a small section of the rope of length $dy$ at a distance of $y$ from the top, as shown in the figure,

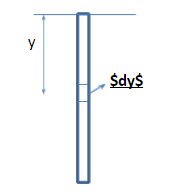
Let A be the area of cross-section of the rope.
Therefore the stain produced on the small section in consideration is =$\dfrac{{\Delta y}}{y}$ ……..(1)
Now weight of the rope is given by –
$
  W = mg \\
  W = \rho Vg \\
 $
Where V is volume of small section in consideration
Since, $V = Ady$
Therefore, $W = \rho Adyg$
Stress produced due to self-weight is given by-
$
  Stress = \dfrac{W}{A} = \dfrac{{\rho Adyg}}{A} \\
   \Rightarrow Stress = \rho gdy \\
 $
Step2: Now using the stress strain equation and substituting all values we get,
Stress$ = $strain$ \times Y$
$
  \rho gdy = \dfrac{{\Delta y}}{y} \times Y \\
  \Delta y = \dfrac{{\rho gy}}{Y}dy \\
 $
Now integrating the above equation,
$
  \Delta y = \int\limits_0^L {\dfrac{{\rho gy}}{Y}dy} \\
  \Delta y = \dfrac{{\rho g}}{Y}\int\limits_0^L {ydy} \\
  \Delta y = \dfrac{{\rho g}}{Y}\left[ {\dfrac{{{y^2}}}{2}} \right]_0^L \\
   \Rightarrow \Delta y = \dfrac{1}{{2Y}}\rho {L^2}g \\
 $

$\therefore$ The increase in the length of the rope due to its own weight is $y = \dfrac{1}{{2Y}}\rho {L^2}g$. Hence option (B) is the correct answer.

Additional information:
Young's modulus is a measure of the ability of a material to withstand changes in length when under lengthwise tension or compression. Its value is always constant for a particular material.

Note:
Keep in mind that stress is not always proportional to the strain. This relation of Hooke's law is only valid up to the proportional limit, beyond that stress is not varying proportional to the strain. Moreover the graph of stress-strain also not remains a straight line after the proportional limit.