Question

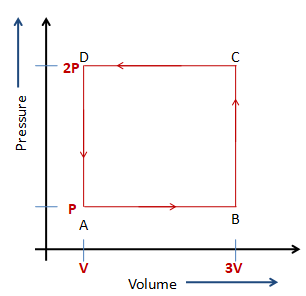
A thermodynamic system is taken through the cycle \[ABCD\] as shown in the figure. Heat rejected by the gas during the cycle is,

\[(A)PV\]
\[(B)2PV\]
\[(C)4PV\]
\[(D)\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em\]

Answer 1

Hint: Find the work done for the whole process using the given pressure and volumes of each point on the graph. Note that the amount of heat rejected from the gas during the cycle.

Formula used:
The work done by gas, $W = P({V_2} - {V_1})$
$P$ is the pressure of a particular point and $({V_2} - {V_1})$ is the change in volume of the gas for that point.
The heat is rejected by the gas $Q = W$.

Complete step by step answer:
The following figure shows the cyclic process of gas.

If an object returns to its initial position after one or more processes it went through.
\[ABCDA\] is the cycle.
The pressure at the points both $D$ and \[C\] remain the same, which is $2P$. The volume at the point $D$ is $V$ and at the point \[C\] is $3V$,
So, the work done by the gas from point $D$ to point \[C\] , ${W_{DC}} = 2P(3V - V) = 4PV$
The pressures at the points $C$ and \[B\]are $2P$ and $P$ respectively. The volume at the points both $C$ and \[B\] remain the same, which is $3V$.
So, the work done by the gas from point $C$ to point \[B\] , ${W_{CB}} = P(3V - 3V) = 0$
The pressure at the points both \[B\] and \[A\] remain the same, which is $P$. The volume at the point \[B\] is $3V$ and at the point \[A\] is $V$,

So, the work done by the gas from point \[B\] to point \[A\] , ${W_{BA}} = P(V - 3V) = - 2PV$
The pressures at the points $A$ and \[D\] are $P$ and $2P$ respectively. The volume at the points both $A$ and \[D\] remain the same, which is $V$.
So, the work done by the gas from point $A$ to the point \[D\] , \[{W_{AD}} = P(V - V) = 0\]
Hence the total work done in the whole cycle, $W = 4PV - 2PV = 2PV$
We know the heat rejected from the cycle is equal to the amount of total work done by the gas, so $Q = W$
$ \Rightarrow Q = 2PV$

Hence, the correct answer is option (B).

Note: In a cyclic process, the total work done can be defined as the area of the portion that is covered by the cycle.
For the given diagram the cycle is \[ABCDA\]
So the work done will be the area of the rectangle \[ABCD\], i.e $W = AB \times BC$
The value will be, $W = (3V - V) \times (2P - P) = 2PV$.