Question

A tetrahedral void in fcc is formed by atoms at:
A. $3$ corners $+$ $1$ face-center
B. $3$ face-centers $+$ $1$ corner
C. $2$ face-centers $+$ $2$ corners
D. $2$ face-center $+$ $1$ corner $+$ $1$ body-center.

Answer 1

Hint:The structure of metals can be explained when atoms are packed together. The atoms in metals are considered as spheres of identical size. Close packing is the most efficient arrangement of spheres of identical size and to fill available spaces in which each sphere touches six neighboring spheres.

Complete step by step answer:
-Crystalline solids are classified into ionic, molecular, metallic and covalent based on their nature of intermolecular forces. A regular $3-\text{D}$ arrangement of points in a space is called a crystal lattice. There are $14$ possible $3-\text{D}$ lattices. They are called Bravais lattices. Each point in a lattice is called a lattice point. Each point in a crystal lattice represents one constituent particle.
-There are three types of centered unit cells-body centered, face centered and end centered. Face centered unit cell contains one constituent particle present at the center of each face, besides the ones that are at its corners. The figure given below depicts a face centered cubic crystal.

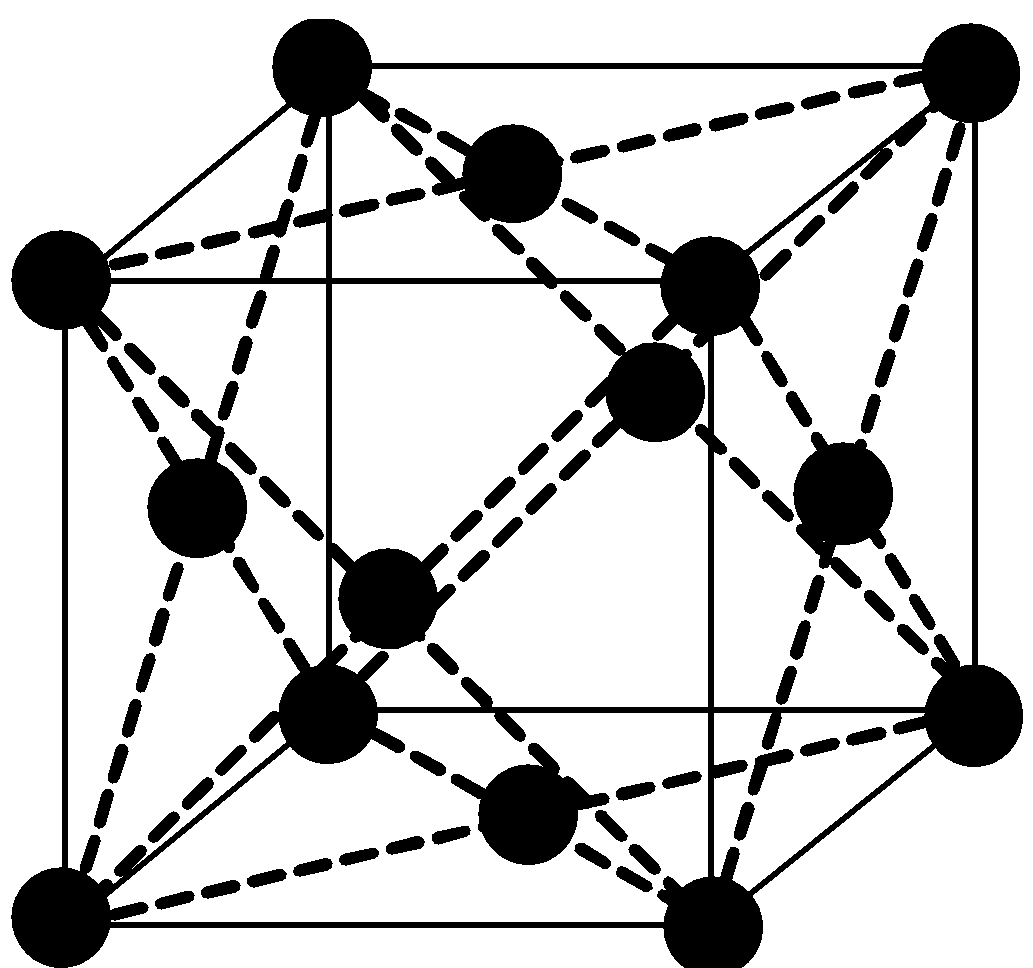
The total number of atoms per unit cell is four in the fcc unit cell.
-Close packing is the most efficient arrangement of spheres of identical size and to fill available spaces in which each sphere touches the neighboring spheres. It is of two types-hexagonal and cubic. It can be explained by considering particles as spheres of identical size arranged in a bottom layer A. When the second layer is placed on layer A, each sphere of layer B will rest in the hollow void in the bottom layer. It produces two types of voids-octahedral and tetrahedral. Tetrahedral void falls above a sphere in the bottom layer.
-Thus we can say that tetrahedral void in fcc is formed by atoms at three corners and one face center It is pictorially represented as given below:
Hence the correct option is A.

Note:
Wherever a sphere of the second layer is above the void of the first layer, a tetrahedral void is formed. The number of tetrahedral voids generated is twice the number of octahedral voids generated. The octahedral void in fcc is formed by atoms at three edges and one center.