Question

A tennis ball is thrown from the height above the ground if the ball strikes to the ground with elastic collision, what height will the ball achieve after the first collision?
$\begin{align}
  & A.\text{ h}{{\text{e}}^{6}} \\
 & B.\text{ }{{\text{e}}^{2}}h \\
 & C.\text{ }{{\text{e}}^{3}}h \\
 & D.\text{ none of these} \\
\end{align}$

Answer 1

Hint: We have been provided a tennis ball which is released at height h and collides on ground. Since the ball is doing elastic collision and we know that in elastic collision, kinetic energy before is equal to kinetic energy after collision. So use conservation of energy and calculate height.

Complete step by step answer:
We have been provided with tennis balls thrown from h height above the ground. Consider when the ball strikes the ground. It possesses elastic collisions. And we need to calculate the height at which ball will reach after the third collision.

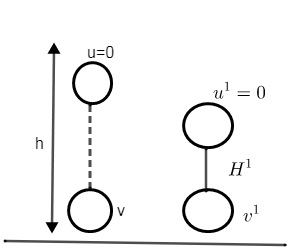
So let’s, consider height h from the ground, a tennis ball is related from the height h, it means initial velocity at a height h is zero. I.e. u=0. Let, v is the velocity of the ball, just before the collision. After collision the velocity of the ball is$v'$. This is a case of elastic collision, energy must have loosed, so ball will go at certain height say ${{h}^{1}}$ which must be less than height h (because of loss of energy)
If you analyse this situation or motion then, only gravitational conservative force is acting. Consider so total mechanical energy will be conserved, in this situation. So, we can say that mechanical energy must be equal at height h just before the collision. Consider ground as reference level so potential energy must be zero. Consider conservation of energy. Total mechanical energy.
Therefore energy before collision = energy after collision (this is for height h)
$\begin{align}
  & mgh+0=0+\dfrac{1}{2}m{{v}^{2}} \\
 & mgh=\dfrac{1}{2}m{{v}^{2}}.....(1) \\
\end{align}$
Let, e is the coefficient of restitution then it is define as ratio of velocity of separation and velocity of approach i.e.
\[\begin{align}
  & e=\dfrac{\text{velocity of separation}}{\text{velocity of approach }} \\
 & e=\dfrac{v'}{v} \\
 & v'=ev.....\left( 2 \right) \\
\end{align}\]
Since collision is elastic collision in case of h’
Therefore, energy before collision = energy after collision
$\begin{align}
  & \Rightarrow \text{ }0+mg{{h}^{1}}=\dfrac{1}{2}mv{{'}^{2}}+0 \\
 & \Rightarrow \text{ }\dfrac{1}{2}m{{\left( ev \right)}^{2}}=mg{{h}^{1}}\text{ }(from\text{ }\left( 2 \right))-\left( 3 \right) \\
\end{align}$
Equation (1) can be written as
$gh=\dfrac{{{v}^{2}}}{2}$
Put this value in equation (3) we get,
$\begin{align}
  & {{h}^{1}}=\dfrac{{{e}^{2}}{{v}^{2}}}{2g}=\dfrac{{{e}^{2}}gh}{g}={{e}^{2}}h \\
 & {{h}^{1}}={{e}^{2}}h.......\left( 4 \right) \\
\end{align}$
So, after the first collision height up to which the tennis ball will reach is ${{e}^{2}}h$.

So, the correct answer is “Option B”.

Note: As you can see in equation (4) height of first collision is equal to height from which we have dropped the tennis ball initially with multiplication of ${{e}^{2}}$. So, when second collision will occur, same procedure or phenomena will be occurring and hence height will decrease with multiplication of square of e (as collision increases) height after second collision is ${{e}^{4}}h$ and hence height after third collision is ${{e}^{6}}h$.
Direction of velocity v is down wards before the collision and direction of $v'$ is upwards after collision.