Question

A telescope has an objective lens of focal length \[150\,{\text{cm}}\] and an eyepiece of focal length of \[5\,{\text{cm}}\]. If a \[50\,{\text{m}}\] tall tower at a distance of \[1\,{\text{km}}\] is observed through this telescope in a normal setting, the angle formed by the image of the tower is \[\theta \], then \[\theta \] is close to.
(A) \[60^\circ \]
(B) \[1^\circ \]
(C) \[30^\circ \]
(D) \[15^\circ \]

Answer 1

Hint: Use the formulae of magnifying power which relates angles and focal lengths. Once we find the magnifying power, then we will find the angle subtended by the object on the objective lens. We will manipulate the expressions accordingly till we find angle subtended by the image at the eyepiece.

Complete step by step answer:
Given,
Focal length of the objective lens is \[150\,{\text{cm}}\] .
Focal length of the eyepiece is \[5\,{\text{cm}}\] .
First of all, we will obtain the expression for the magnifying power of the telescope, which is given by:
\[MP = \dfrac{\beta }{\alpha }\] …… (1)
Where,
\[MP\] indicates the magnifying power.
\[\beta \] indicates the angle subtended by the image at the eyepiece.
\[\alpha \] indicates the angle subtended by the object on the objective lens.
For the small angle, we can write the angle as the tangent of that angle itself i.e. we can write:
\[\tan \alpha = \alpha \]
\[\tan \beta = \beta \]
Substituting these values, we can modify the equation (1) as:
\[MP = \dfrac{\beta }{\alpha }\]
Again, magnifying power of a telescope can be written alternatively as:
\[MP = \dfrac{{{f_o}}}{{{f_e}}}\] …… (2)
Where,
\[{f_o}\] indicates the focal length of the objective lens.
\[{f_e}\] indicates the focal length of the eye piece.
Substituting, \[{f_0} = 150\,{\text{cm}}\] and \[{f_e} = 5\,{\text{cm}}\] in the equation (2), we get:
\[
MP = \dfrac{{{f_o}}}{{{f_e}}} \\
\Rightarrow MP= \dfrac{{150}}{5} \\
\Rightarrow MP= 30 \\
\]
We are given, that the height of the tower is \[50\,{\text{m}}\] and the distance of the tower from the objective is \[1\,{\text{km}}\] i.e.\[1000\,{\text{m}}\].It can be shown with a simple diagram below:

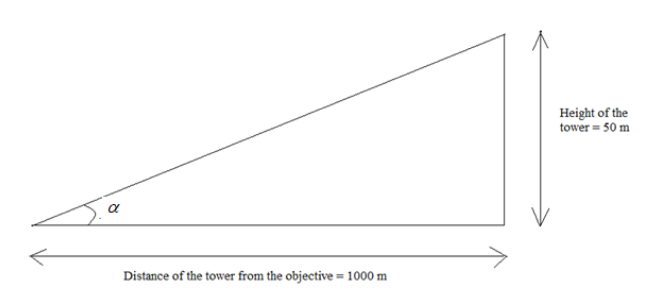
Applying, tangent in the above figure:
\[
\tan\alpha = \dfrac{{50}}{{1000}} \\
\Rightarrow\tan\alpha= \dfrac{1}{{20}}\, \\
\]
According to the question,
Angle formed by the image of the tower is \[\theta \].We can write,
\[\tan \beta = \tan \theta \] …… (3)
Again, from equation (1), we can write:
\[\tan \beta = MP \times \tan \alpha \]
\[
\Rightarrow\tan \beta = MP \times \tan \alpha \\
\Rightarrow\tan \beta = 30 \times \dfrac{1}{{20}} \\
\Rightarrow\tan \beta = \dfrac{3}{2} \\
\Rightarrow\tan \beta = 1.5 \\
\]
From equation (3):
\[
\tan \theta = 1.5 \\
\Rightarrow\theta = {\tan ^{ - 1}}\left( {1.5} \right) \\
\therefore\theta = 56.31^\circ \\
\]
Angle formed by the image of the tower is \[56.31^\circ \].But in the options, none of them exactly match with the value found, but \[60^\circ \] is closer to it.

Hence, the correct option is (A).

Note: While solving this problem, you should have a clear understanding about the magnifying power of the telescope and its various expressions. While calculating the trigonometric ratio “tangent” remember that its perpendicular over base. To find the answer correctly in degrees, you have to take an inverse trigonometric ratio.