Question

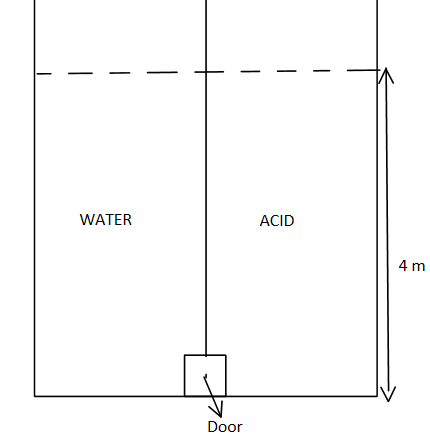
A tank with a square base of area $1\,{m^2}$ is divided by a vertical partition in the middle. The bottom of the partition has a small hinged door of area $20\,c{m^2}$ the tank is filled with water in a compartment and an acid (of relative density $1.7$ ) in the other , both to the height of $4\,m$. Compute force necessary to keep the door closed.
A. Force required to close the door$ = 54.8\,N$

Answer 1

HintThe given problem is based on the concept of pressure and pressure difference.
Remember the pressure,
$P = h\rho g$
And Force$ = $Pressure $ \times $Area

 Complete step-by-step solution:Form the problem we have
Tank (square) base area $ = 1\,{m^2}$
Door area $ = 20\,c{m^2} = 20 \times {10^{ - 4}}\,{m^2}$
Density of water $ = {10^3}\,kg/{m^3}$
Relative density of acid $ = 1.7$

Since relative density$ = \dfrac{{density\,of\,acid}}{{density\,of\,water}}$
$\therefore $Density of acid $ = 1.7 \times {10^3}\,kg/{m^3}$
First calculate the pressure difference
$\vartriangle P = $Pressure of acid $ - $ Pressure of water
$
  \vartriangle P = \left( {1.7 \times {{10}^3} \times 9.8 \times 4} \right) - \left( {{{10}^3} \times 9.8 \times 4} \right) \\
  \vartriangle P = \left( {0.7 \times {{10}^3} \times 9.8 \times 4} \right) \\
 $
Since we know
Force $ = $ Pressure $ \times $ Area
The force on the door with area $20 \times {10^{ - 4}}\,{m^2}$ is,
$
  F = \left( {0.7 \times {{10}^3} \times 9.8 \times 4} \right)\left( {20 \times {{10}^{ - 4}}} \right) \\
  F = 54.8\,N \simeq \,55\,N \\
 $

Note:
1) The problem related to liquid mainly relates with pressure and factors which affect the pressure.
2) Relation between relative density and density of material are useful terms so revise them carefully