Question

A system of three polarizers ${{P}_{1}},{{P}_{2,}}{{P}_{3}}$ is set up such that the pass axis of ${{P}_{3}}$ is crossed with respect to that of${{P}_{1}}$. The pass axis of ${{P}_{2}}$ is inclined at ${{60}^{o}}$ to the pass axis of ${{P}_{3}}$when a beam of unpolarized light of intensity ${{I}_{O}}$ is incident on ${{P}_{1}}$the in of light transmitted by three polarized I. the ratio $\left( \dfrac{{{I}_{o}}}{I} \right)$ equals (nearly):
$\begin{align}
  & A.16.00 \\
 & B.1.80 \\
 & C.5.33 \\
 & D.10.67 \\
\end{align}$

Answer 1

Hint: According to the malu’s law the intensity of the plane polarized light passing through a second polarized (also called as analyzers) is directly proportional to cosine of angle between axes of two polarizers when an unpolarized light is incident on a polarizer the intensity of light transmitted will always be half of the incident light.

Complete answer:

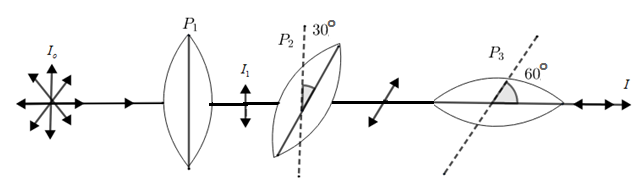
Given that intensity of light falling on polarizers ${{P}_{1}}$ and ${{I}_{O}}$. The intensity of light coming out from polarizer ${{P}_{3}}$ is I. so we have to find out ratio $\left( \dfrac{{{I}_{o}}}{I} \right)$ i.e. ratio of intensity of incident light to intensity of transmitted light from the polarizer ${{P}_{3}}$. Also given that the incident light is unpolarized i.e. electric field in the incident light varies in all directions.
When this unpolarized light is incident on polarized ${{P}_{1}}$, the transmitted light through ${{P}_{1}}$ will be linearly polarized in which plane of vibration will in the plane of axis of polarizer. Therefore, the intensity of light that is transmitted through ${{P}_{1}}$ will be half of the intensity of incident light.
Let ${{I}_{1}}$ be the intensity of light that is transmitted through ${{P}_{1}}$
$\therefore {{I}_{1}}=\dfrac{{{I}_{o}}}{2}$
This light will fall on the polarizer ${{P}_{2}}$
Given that the pass axis of ${{P}_{3}}$is crossed with the respect to that of ${{P}_{1}}$
Therefore the angle between the axis of polarizer ${{P}_{1}}$ and polarizer ${{P}_{3}}$ is ${{90}^{o}}$ also, the pass axis of ${{P}_{2}}$ is inclined at ${{60}^{o}}$ to the pass axis of ${{P}_{3}}$ therefore the angle between ${{P}_{2}}\text{ and }{{P}_{3}}$ is. Thus the angle between axes of polarizer ${{P}_{1}}$ and ${{P}_{2}}$ will be ${{30}^{o}}$. Let ${{I}_{2}}$ be the intensity of light transmitted through polarized ${{P}_{2}}$
Therefore according to Malus law
$\begin{align}
  & {{I}_{2}}={{I}_{1}}{{\cos }^{2}}{{30}^{o}} \\
 & =\dfrac{{{I}_{o}}}{2}\times \dfrac{3}{4} \\
 & {{I}_{2}}=\dfrac{3}{8}{{I}_{o}} \\
\end{align}$

Similarly the intensity of light that is transmitted through polarizer ${{P}_{3}}$ is
$\begin{align}
 & I={{I}_{2}}{{\cos }^{2}}{{60}^{o}} \\
 & \dfrac{3}{8}{{I}_{o}}\times \dfrac{1}{4} \\
 & I=\dfrac{3}{32}{{I}_{o}} \\
 & \therefore \dfrac{{{I}_{o}}}{I}=\dfrac{32}{3} \\
 & \dfrac{{{I}_{o}}}{I}=10.67 \\
\end{align}$
Thus, the ratio $\left( \dfrac{{{I}_{o}}}{I} \right)$ equals 10.67. Therefore the correct option is (D).

So, the correct answer is “Option d”.

Note:
Malu’s law helps to understand the polarization properties of light. This law gives the relation between intensity of light fall on a polarizer and the intensity of light transmitted through a same polarizer. Carefully take the angle students may get confused when plane polarized light is incident on a polarizer. In that case you have to consider the angle between the plane of polarization of incident light and the axis of the polarizer.