Question

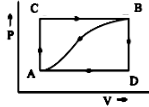
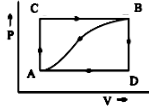
When a system is taken from state A to state B along the path ACB, ${ 80J }$ of heat flows into the system and the system does ${ 30J }$ of work.
(A) How much heat flows into the system along the path ADB if the work done is ${ 10J }$?
(B) When the system is returned from state B to A along the curved path, the work done on the system is ${ 20J }$. Does the system absorb or liberate heat, and how much?
(C) If ${ U }_{ D }{ -U }_{ A }{ =40J }$. Find the heat absorbed in the process AD and DB.

Answer 1

Hint: Open system is defined as the one that permits the exchange of both matter and energy among systems and surroundings. The closed system allows the exchange of energy but not matter. As heat is supplied that is given to the system but no matter is exchanged, it is a closed system.

Complete step by step solution:
The internal energy of any system is the total of all the kinds of energy present in the system. It does not depend on the path but only on the state of the system and hence it is a state function.
Since ${ \Delta U }$ is independent of path.
According to the first law of thermodynamics, ${ \Delta U=q-w }$......(1)
where, ${ \Delta U }$ = change in internal energy
q = heat added to the system
w = work done by the system

Therefore, ${ \Delta U(A\rightarrow B) }$ = q(ACB) + w(ACB)
                                            = ${ 80 - 30 = 50J }$
(A) It is given that,
${ \Delta U }$ = ${ 50J }$
w = work done on the system is ${ 10J }$
So, By using the equation (1), we get
${ \Delta U }$ = q(ADB) + w(ADB)
From here we can calculate the heat flows into the system,
 q(ADB) = ${ 50 - (10) = 40J }$.
Hence, the heat flows into the system along the path ADB = ${ 40J }$.

(B) It is given that,
Work done on the system = ${ 20J }$
Change in internal energy = ${ 50J }$
Using the above formula, we can calculate heat flows from B to A,
q ${ (B\rightarrow A) }$ = ${ \Delta U }$ ${ (B\rightarrow A) }$ -w ${ (B\rightarrow A) }$
                          = ${ -50 - (20) = -70J }$
Since, ${ \Delta U }$ ${ (A\rightarrow B) }$ = - ${ \Delta U }$ ${ (B\rightarrow A) }$
Hence, the system liberates energy that is ${ -70J }$.

(C) ${ \Delta U }$ (ADB) = ${ \Delta U(A\rightarrow D)+\Delta U(D\rightarrow B) }$
${ \Delta U(D\rightarrow B) }$ = ${ 50J - 40J = 10J }$.
Again,
${ \Delta U(D\rightarrow B) }$ = ${ q(D\rightarrow B)+w(D\rightarrow B) }$
Since ${ V(D\rightarrow B) }$ is constant
where V= volume
Therefore, w ${ (D\rightarrow B) }$ = constant [ work done on the system is constant if the volume is constant].
Therefore, q ${ (D\rightarrow B) }$
${ \Delta U(D\rightarrow B) }$ = 10J
Now,
q(ADB) = q ${ (A\rightarrow D) }$ + q ${ (D\rightarrow B) }$
${ q(A\rightarrow D) }$ = ${ 40 - 30 = 10J }$ [q(ADB) = 40J]
Hence, the heat absorbed in the process AD and DB is ${ 10J }$.

Note: The possibility to make a mistake is that if the system is absorbing heat means heat is added to it then heat is considered positive whereas the work done by the system is negative, not positive.