Question

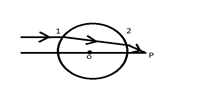
A sunshine recorder globe of 30cm diameter is made of glass of $\mu = 1.5$. A ray enters the globe parallel to its axis. Find the position from the centre of the sphere, where the ray crosses the axis.

Answer 1

Hint:Here the above question deals with two medium air and glass. Hence we have to find the image and object distance at the two surfaces A and B. apply the relation between the object distance $u$, image distance $v$, refractive index $n$ and radius of curvature $R$ for refraction at a spherical surface. Apply the given data to obtain the position from the centre of the sphere

Formula Used:
$\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R}$
Here$u$,$v$,$R$,$n$are object distance ,image distance, radius of curvature and refractive index

Complete step by step answer:
Bending of a light wave passing through one medium to another medium due to the change in wave speed is the Refraction. The ray bends towards the normal, when a light travels from a rarer medium to a denser medium.
For lenses the sign convention:
Focal length of a convex lens is positive and for a concave lens is negative.
The optical centre is taken by all the measurements.
All measurements are taken from the optical centre.
Optical centre of a lens lies on the origin of the x-y axis.
Here the light undergoes refraction twice. The incident light gets refracted at surface 1, that light gets refracted again at surface 2.
Let us first consider the surface 1, here ${n_1} = 1$ and ${n_2} = 1.5$.
$\dfrac{{1.5}}{v} - \dfrac{1}{{ - \infty }} = \dfrac{{1.5 - 1}}{{15}}$
$v = \dfrac{{15 \times 1.5}}{{0.5}}$
$v = 45cm$
For the second surface, here${n_1} = 1.5$,${n_2} = 1$; The image formed on surface 1 acts as the object for surface 2.

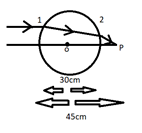
Hence the object distance $u = 45 - 30 = 15cm$
$\dfrac{1}{v} - \dfrac{{1.5}}{{15}} = \dfrac{{1 - 1.5}}{{ - 15}}$
$v = \dfrac{{15}}{2} = 7.5cm$

Hence the position from the centre of the sphere $ = 15 + 7.5 = 22.5cm$

Note:While solving problems relating to lenses, we should take proper care of the signs of different quantities. The magnification is defined as the ratio of the height of the image to that of the height of the object. Lens formula gives the relationship between object distance, image distance and the focal length.