Question

A string is stretched by a suspended weight of density ρ immersed in a liquid of density σ. Find the velocity of the transverse wave in the string.

Answer 1

Hint: We have to find the velocity of a transverse wave in the string which is stretched by a suspended weight immersed in a liquid. Here we will find the velocity the tension experienced by string due to the suspended weight. To calculate tension we will find the force experienced by the suspended weight.

Formula used:
\[\begin{align}
  & {{F}_{b}}=\sigma {{V}_{d}}g \\
 & v=\sqrt{\dfrac{T}{\mu }} \\
\end{align}\]

Complete answer:
Let us first draw a diagram for the given question

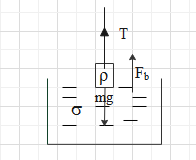
Here T is the tension in the string due to the suspended weight of density ρ and the weight is immersed in liquid whose density is given as σ.
Now according to Archimedes’ principle there will be buoyancy or upthrust experienced by the suspended weight when immersed into the liquid. This upthrust or upward force on the suspended weight can be given as
\[{{F}_{b}}=\sigma {{V}_{d}}g\]
Where σ is the density of the liquid, \[{{V}_{d}}\] is the volume of liquid displaced and g is the acceleration due to gravity.
If m is the mass of the suspended weight then the downward pull experienced by it is given as mg. Now balancing all the forces on the suspended weight we get
\[\begin{align}
  & T={{F}_{b}}-mg \\
 & \Rightarrow T=\sigma {{V}_{d}}g-mg \\
 & \Rightarrow T=g\left( \sigma {{V}_{d}}-\rho V \right) \\
\end{align}\]
Now mass of the suspended weight can be written as a product of density and its volume. Density of suspended weight is given and if V is the volume of the suspended weight then, the mass can be written as
\[m=\rho V\]
Substituting it we get
\[T=g\left( \sigma {{V}_{d}}-\rho V \right)\]
Now the velocity of transverse wave is given as
\[v=\sqrt{\dfrac{T}{\mu }}\]
Where T is the tension and μ is the linear density. Linear density is the mass per unit length.
Now we know the tension experienced by string (which we calculated above). Substituting it in the above formula we will get the transverse velocity for the string. Hence, we can write
\[v=\sqrt{\dfrac{g\left( \sigma {{V}_{d}}-\rho V \right)}{\mu }}\]
Hence we got an expression of velocity of transverse wave of string in terms of density of the suspended weight and the density of liquid in which the weight was immersed.

Note: Weight and mass are different quantities. Here weight is the force which is experienced due to gravity or due to the mass of an object. Also the weight of an object can vary with respect to surface but mass remains the same. Linear density is also different from density as linear density is mass per unit length whereas density is mass per unit volume.