Question

A straight line has a slope of 0. How do you write one possible equation that might represent this line?

Answer 1

Hint: Try to frame the equation as reference to the slope intercept form. As given that the slope is 0, the equation will only contain the ‘y’- intercept ‘c’ which can be any positive or negative value of your choice.

Complete step-by-step answer:
Slope intercept form: We know a general straight line has an equation in the form $y=mx+c$, where ‘m’ is the slope and ‘c’ is the intercept with the y-axis.
Since it is given that the slope is 0
So for our equation, $m=0$
And as its slope is 0, so it is a constant which never changes and can intercept the y-axis at any point.
Hence the form of our equation is
$\begin{align}
  & y=mx+c \\
 & \Rightarrow y=0\times x+c \\
 & \Rightarrow y=0+c \\
 & \Rightarrow y=c \\
\end{align}$
Here ‘c’ can be any positive or negative value.
Let $c=-4$
So our equation can be written as $y=-4$
This is our required equation.
Since this is a constant function so for every value of ‘x’ there is always the same value of ‘y’ i.e. $-4$ .

Note: Equation should be framed by taking the reference of slope intercept form of the straight line. ‘c’ could take any positive or negative value. Since we have the constant value of $y=-4$ so we can graph the equation by taking the value of ‘x’ as anything, say 1,2,3…

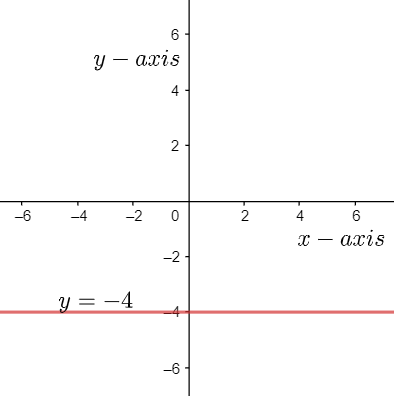
From the above graph we can conclude that $y=-4$ is a straight line passing through the point $\left( 0,-4 \right)$ and parallel to the x-axis.