Question

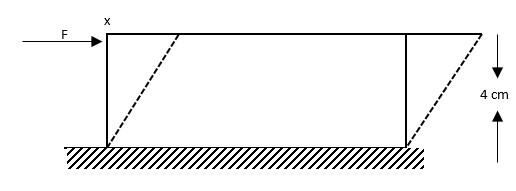
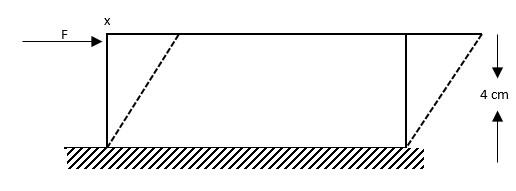
A steel plate of face area $1c{m^2}$ and thickness $4cm$ is fixed rigidly at the lower surface. A tangential force $F = 10kN$ is applied on the upper surface as shown in the figure. The lateral displacement $x$ of upper surface w.r.t the lower surface is (Modulus of rigidity for steel is $8 \times {10^{11}}N/{m^2}$ ?

Answer 1

Hint: Concept of Modulus rigidity will be used which is the ratio of stress to the longitudinal strain within the elastic limit. Firstly collect the data and apply formula of Modulus of rigidity $(\eta ).$

Given that: Tangential forced (f)$ = 10KN$
$ F = 10KN = 10 \times {10^3} (\because LKN = {10^3}N) $
Thickness of plate $ = L = 4\,cm = 4 \times {10^{ - 2}}m.$
Area of steel plate $ = A = 1\,c{m^2} = {10^{ - 4}}{m^2}$
Modulus of rigidity $ = \eta = 8 \times {10^{11}}N/{m^2}$
Later displacement $ = \Delta L = ?$
Now formula used:
$\eta = \dfrac{{F \times L}}{{A \times \Delta L}}$
Where $\eta = $Modulus of rigidity
F$ = $force on plate
L$ = $thickness of plate
A$ = $area of plate
\[
  \eta = \dfrac{{10 \times {{10}^3} \times 4 \times {{10}^{ - 2}}}}{{{{10}^{ - 4}} \times \Delta L}} \\
  8 \times {10^{11}} = \dfrac{{{{10}^4} \times 4 \times {{10}^{ - 2}}}}{{{{10}^{ - 4}} \times \Delta L}} \\
  \Delta L = \dfrac{{4 \times {{10}^2}}}{{{{10}^{ - 4}} \times 8 \times {{10}^{11}}}} \\
  \Delta L = \dfrac{4}{8} \times {10^{ - 5}} = 0.5 \times {10^{ - 5}} = 5 \times 10 \times - 6 \\
 \]

So, the correct answer is “Option A”.

Note:
 After applying the formula $\eta =\dfrac{F}{A}\dfrac{L}{{\Delta L}}$ and put the value at lateral displacement. Where F/A is the stress applied and there is corresponding strain to it.