Question

A statue 4 meters high sits on a column 5.6 meters high. How far from the column must a man, whose eye level is 1.6 meters from the ground, stand in order to have the most favorable view of the statue.

Answer 1

Hint: First, draw the figure on the base of data provided. Then find the value of $\tan \beta $ from triangle BCD. After that, find the value of $\tan \alpha $ from the triangle ABC by using formula $\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}$. After that differentiate the terms with respect to $x$ and equate with 0 to maximize the function for a favorable view. Then solve for $x$.

Complete step-by-step answer:
To find:- The distance between the column and man.
Let the distance between the column and man be x.
The figure for the problem is,

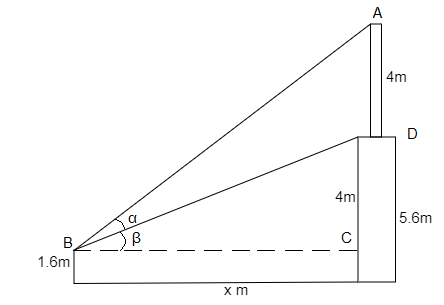
In $\Delta BCD$,
$\tan \beta = \dfrac{{BD}}{{BC}}$
Substitute the value of BD and BC,
$\tan \beta = \dfrac{4}{x}$ ….. (1)
In $\Delta ABC$,
$\tan \left( {\alpha + \beta } \right) = \dfrac{{AC}}{{BC}}$
Since $AC = AD + DC$. Then,
$\tan \left( {\alpha + \beta } \right) = \dfrac{{AD + DC}}{{BC}}$
Substitute the values of AD, DC, and BC,
\[\tan \left( {\alpha + \beta } \right) = \dfrac{{4 + 4}}{x}\]
As we know that $\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}$. So,
$\dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} = \dfrac{8}{x}$
Substitute the value of $\tan \beta $ from equation (1),
$\dfrac{{\tan \alpha + \dfrac{4}{x}}}{{1 - \tan \alpha \times \dfrac{4}{x}}} = \dfrac{8}{x}$
Multiply the denominator of the left side on the right side,
$\tan \alpha + \dfrac{4}{x} = \dfrac{8}{x} - \dfrac{{32}}{{{x^2}}}\tan \alpha $
Move $\dfrac{{32}}{{{x^2}}}\tan \alpha $ on the left side and $\dfrac{4}{x}$ on the right side,
$\tan \alpha + \dfrac{{32}}{{{x^2}}}\tan \alpha = \dfrac{8}{x} - \dfrac{4}{x}$
Take $\tan \alpha $ common from the left side and subtract the terms on the right side,
$\tan \alpha \left( {1 + \dfrac{{32}}{{{x^2}}}} \right) = \dfrac{4}{x}$
Divide both sides by $\left( {1 + \dfrac{{32}}{{{x^2}}}} \right)$,
$\tan \alpha = \dfrac{{\dfrac{4}{x}}}{{\left( {1 + \dfrac{{32}}{{{x^2}}}} \right)}}$
Take LCM in the denominator,
$\tan \alpha = \dfrac{{\dfrac{4}{x}}}{{\left( {\dfrac{{{x^2} + 32}}{{{x^2}}}} \right)}}$
Cancel out the common factors,
$\tan \alpha = \dfrac{{4x}}{{{x^2} + 32}}$
For the most favorable view, we have to maximize $\theta $. Since $\theta \in \left( {0,\dfrac{\pi }{2}} \right]$.
Let $t\left( x \right) = \tan \theta $,
$\operatorname{t} \left( x \right) = \dfrac{{4x}}{{{x^2} + 32}}$
Differentiate with respect to $x$.
$\dfrac{d}{{dx}}\left[ {t\left( x \right)} \right] = \dfrac{d}{{dx}}\left( {\dfrac{{4x}}{{{x^2} + 32}}} \right)$
As we know that, $\dfrac{d}{{dx}}\left[ {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}} \right] = \dfrac{{g\left( x \right)f'\left( x \right) - f\left( x \right)g'\left( x \right)}}{{{{\left[ {g\left( x \right)} \right]}^2}}}$. Then,
$\dfrac{d}{{dx}}\left[ {t\left( x \right)} \right] = \dfrac{{\left( {{x^2} + 32} \right) \times 4 - 4x\left( {2x} \right)}}{{{{\left( {{x^2} + 32} \right)}^2}}}$
Open the brackets and multiply the terms. For maximum substitute $\dfrac{d}{{dx}}\left[ {t\left( x \right)} \right] = 0$.
$\dfrac{{4{x^2} + 128 - 8{x^2}}}{{{{\left( {{x^2} + 32} \right)}^2}}} = 0$
Subtract the like terms in the numerator and multiply the denominator to the right side,
$128 - 4{x^2} = 0$
Move the variable on the other side,
$4{x^2} = 128$
Divide both sides by 4,
${x^2} = 32$
Take the square root on both sides,
$x = \pm \sqrt {32} $
Since, distance cannot be negative,
$x = 4\sqrt 2 \,{\text{m}}$

Hence, the distance between the column and man is $4\sqrt 2 \,{\text{m}}$.

Note: The ratio should exist between the quantities of the same kind.
While comparing two things, the units should be similar.
There should be significant order of terms.
The comparison of two ratios can be performed, if the ratios are equivalent to the fractions.