Question

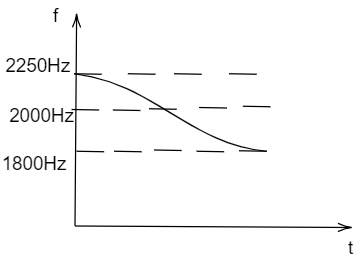
A stationary observer receivers a sound of frequency $ 2000{\text{ }}Hz $ . The variations of apparent frequency and time is shown. Find the speed of source, if velocity of sound is $ 300\dfrac{m}{s} $ .

(A) $ \;66.6\dfrac{m}{s} $
(B) $ \;33.3\;\dfrac{m}{s} $
(C) $ 27.3\;\dfrac{m}{s} $
(D) $ 59.3\;\dfrac{m}{s} $

Answer 1

Hint : As the source moves towards the observer the apparent frequency increases and as the source moves away from the observer the apparent frequency decreases. The Doppler Effect states that the frequency of the sound wave changes with respect to an observer who is in motion relative to the source.

Formula used:
 $\Rightarrow {f_m} = \dfrac{{v + {v_o}}}{{v - {v_s}}} \times f $
Where $ {f_m} $ is the maximum frequency, $ v $ is the velocity of sound, $ {v_o} $ is the velocity of the observer, $ {v_s} $ is the velocity of sound, and $ f $ is the original frequency of the source.

Complete step by step answer
It is given that $ {v_o} = 0\dfrac{m}{s} $ , $ v = 300\dfrac{m}{s} $ , $ f = 2000Hz $ , $ {f_m} = 2250Hz $
We need to find the value of $ {v_s} $ .
From the Doppler Effect of sound wave,
 $\Rightarrow {f_m} = \dfrac{{v + {v_o}}}{{v - {v_s}}} \times f $
Where $ {f_m} $ is the maximum frequency, $ v $ is the velocity of sound, $ {v_o} $ is the velocity of the observer, $ {v_s} $ is the velocity of sound, and $ f $ is the original frequency of the source.
Substituting the known values in the above equation,
 $\Rightarrow 2250Hz = \dfrac{{300 + 0}}{{300 - {v_s}}} \times 2000Hz $
 $\Rightarrow {v_s} = 300 - \dfrac{{300 \times 2000}}{{2250}} $
 $\Rightarrow {v_s} = 300(1 - \dfrac{{2000}}{{2250}}) $
On further calculation,
 $\Rightarrow {v_s} = 33.3333\dfrac{m}{s} $
Hence the correct answer to the given question is (B) $ \;33.3\;\dfrac{m}{s} $ .

Additional Information
A common example of Doppler shift is the change of pitch which the observer seems to hear when a vehicle producing sound approaches and recedes from an observer. The emitted frequency is lower than the received frequency when the vehicle approaches, identical at the instant of passing by, and higher during the recession.

Note
In the above question we were discussing only the Doppler Effect of sound waves but it is not limited to sound waves. The Doppler Effect is also applicable for light waves i.e. electromagnetic waves. It has very diverse applications like robotics, sirens, astronomy, radar, satellites, acoustics, the healthcare system, and many more.