Question

A square tin sheet of side $ 12 $ inches is converted into a box with an open top in the following steps the sheet is placed horizontally. Then, equal sized squares, each side $ x $ inches, are cut from the four corners of the sheet. Finally, the four resulting sides are bent vertically upwards in the shape of a box. If $ x $ is an integer, then what value of x maximizes the volume of the box?

Answer 1

Hint: In this question we have to find the volume of the cuboid and differentiate it to get the value of $ x $ maximizes the volume of the box. Also apply the method of factorization.

Complete step-by-step answer:
After conversation sheet in the form of a box it becomes a cuboid so

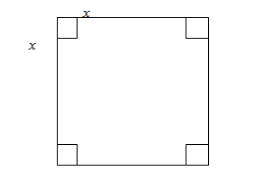
Length of the box will be \[ = 12 - x - x\]
 $ = 12 - 2x $ Inches
Breadth of the box will be $ = 12 - x - x $
 $ = 12 - 2x $ Inches
Height of the box will be $ = x $ Inches
 We know that volume of cuboid $ = length \times breadth \times height $
 $ = \left( {12 - 2x} \right) \times \left( {12 - 2x} \right) \times x $
 $ = \mathop {\left( {12 - 2x} \right)}\nolimits^2 x $
 $ = \left( {144 + 4\mathop x\nolimits^2 - 2 \times 12 \times 2x} \right)x $
 $ = 144x + 4{x^3} - 48{x^2} $
Here volume of the cuboid $ V = 144x + 4{x^3} - 48{x^2} $
Now differentiation of volume of the cuboid with the respect of $ x $ we get.
\[\dfrac{{dv}}{{dx}} = \dfrac{d}{{dx}}\left( {144x + 4\mathop x\nolimits^3 - 48\mathop x\nolimits^2 } \right)\]
 $ = \dfrac{d}{{dx}}144x + \dfrac{d}{{dx}}4\mathop x\nolimits^3 - \dfrac{d}{{dx}}48\mathop x\nolimits^2 $
 $ = 144\dfrac{d}{{dx}}x + 4\dfrac{d}{{dx}}\mathop x\nolimits^3 - 48\dfrac{d}{{dx}}\mathop x\nolimits^2 $
 $ = 144 + 12\mathop x\nolimits^2 - 96x $
 $ = \mathop x\nolimits^2 - 8x + 12 $
After factorization of this we get.
 $ x = 6,2 $
Putting $ x = 6 $ in the volume of cuboid we get,
 $ = 144 \times 6 + 4 \times \mathop {\left( 6 \right)}\nolimits^3 - 48 \times \mathop {\left( 6 \right)}\nolimits^2 $
 $ = 0 $
Putting $ x = 2 $ in the volume of cuboid we get
 $ = 144 \times 2 + 4\mathop {\left( 2 \right)}\nolimits^3 - 48\mathop {\left( 2 \right)}\nolimits^2 $
 $ = 128 $ Inches
Hence the value of $ x $ in this question is $ 2 $ and volume of the tin sheet is $ 128 $ inches
So, the correct answer is “ $ x $ in this question is $ 2 $ and volume of the tin sheet is $ 128 $ inches”.

Note: In this question the bent shape of the box looks like a cuboid. A cuboid is a three-dimensional shape which has six faces, which form a convex polyhedron. Be careful while understanding the word statements and letters, read it twice, do simplification and solve using the mathematical operations.