Question

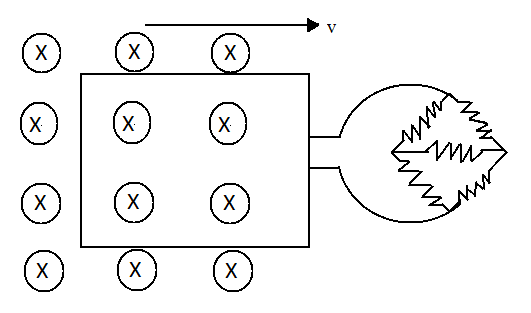
A square metal loop of side $10cm$ and resistance $1\Omega $ is moved with a constant velocity partly inside a uniform magnetic field of $2Wb\,{m^{ - 2}}$ , directed into the plane of paper, as shown in the figure. The loop is connected to a network of five resistors each of value $3\Omega $ . If a steady current of $1mA$ flows in the loop, then the speed of the loop is

A) $0.5cm\,{s^{ - 1}}$
B) $1cm\,{s^{ - 1}}$
C) $2cm\,{s^{ - 1}}$
D) $4cm\,{s^{ - 1}}$

Answer 1

Hint:First calculate the effective resistance of the entire circuit (the wheat-stone bridge and the square loop) and then use the formulas for induced EMF ( $\varepsilon $) and equate all the given values to find the velocity of the loop.

Formulas Used:
Induced EMF, $\varepsilon = Bvl = IR$
Where $B$ is the magnitude of the magnetic field, $v$ is the velocity of the loop, $l$ is the side length of the square loop, $I$ is the current in the loop, and $R$ is the net resistance of the entire loop.

Step by step Solution:
First, we will calculate the net resistance of the loop. The given network of resistors forms a wheat-stone bridge. Therefore, the resistor in the middle will be neglected as it will have no effect on the circuit. We will calculate the total resistance by the remaining resistors.
There are $4$ resistors, there is a pair of two $3\Omega $ resistors in series which are connected in parallel.
Let net resistance in two $3\Omega $ resistors in series be ${R_1}$
Therefore, ${R_1} = 3 + 3 = 6\Omega $
The other pair of $3\Omega $ resistors are also in series. Therefore, ${R_2} = 6\Omega $
Let the net resistance of this wheat-stone bridge be ${R'}$. Therefore, $\dfrac{1}{{{R'}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} = = \dfrac{1}{6} + \dfrac{1}{6} = \dfrac{2}{6} = \dfrac{1}{3}$
$ \Rightarrow {R'} = 3\Omega $
The wheat-stone bridge and the square loop are in series. Therefore, the total resistance of the entire circuit will be the sum of these two i.e. $R = 1 + 3 = 4\Omega $.
Now, let the speed of the loop be $v$ .
Current in the loop, $I = 1mA = 0.001A$
Side of the square loop, $l = 10cm = 0.1m$
Magnetic strength given, $B = 2Wb\,{m^{ - 2}}$
We know that induced EMF of a circuit, $\varepsilon = IR$
Also, $\varepsilon = Bvl$
Using these two, we get $Bvl = IR$
On putting the values, $2 \times v \times 0.1 = 0.001 \times 4$
$ \Rightarrow v = \dfrac{{0.004}}{{0.2}} = 0.02m{s^{ - 1}}$
This is the required answer.

Note: Always convert the given values into SI units before use. In a wheat-stone bridge, the resistance in the middle of other four resistances has zero effect on the circuit as its resistance gets cancelled out and hence, it can be neglected to make our calculations easier.