Question

A square lawn is surrounded by a path 2.5m wide. If the area of path is 165 \[{{m}^{2}}\], find the area of the lawn?

Answer 1

Hint: Area of a square of side length a meter is given by \[{{a}^{2}}\] square meters.
Area of a rectangle with length l and breadth b is given by (l x b) square meters. Area of a shape which is a combination of two shapes of area m and n square meters respectively is given by (m + n) square meters.

Complete step-by-step solution:
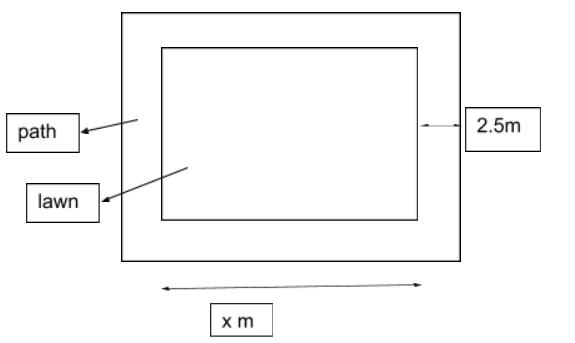
According to the question, the width of the path surrounding the lawn is 2.5 meter. The area of this path is given as 165 square meters.
Consider the side of the lawn to be x. Then the side of the lawn including the path is x+2(2.5) which is simply x+5 meter. Refer the figure given below:

We know that,
(Area of lawn including the path) = (Area of the lawn alone) + (Area of the path)
From this we can write,
(Area of the lawn) = (Area of lawn including path) – (Area of the path)
Then as per the question,
\[{{x}^{2}}={{(x+5)}^{2}}-165\]
\[\Rightarrow {{x}^{2}}=({{x}^{2}}+10x+25)-165\]
\[\Rightarrow {{x}^{2}}={{x}^{2}}+10x+25-165\]
\[\Rightarrow {{x}^{2}}={{x}^{2}}+10x-140\]
\[\Rightarrow {{x}^{2}}-{{x}^{2}}-140=-10x\]
\[\Rightarrow -140=-10x\]
Which means 140=10x
\[\therefore x=\dfrac{140}{10}=14\]
Therefore, the side length of the lawn is 14 meter.
So, the area of the lawn = \[{{x}^{2}}={{(14)}^{2}}=196\] square meters.

Note: This type of problem can be solved by dividing like: if the width of the path is w meter and its area be y square meters. Let x be the side length of the lawn, then y will be given by y = 2(xw) + 2w(x+2w) which is simply \[y=4xw+4{{w}^{2}}\] from this we get the value of x, side length of the lawn.