Question

A square lawn is bounded on three sides by a path $4\,m$ wide. If the area of the path is $\dfrac{7}{8}$ that of the lawn, find the dimensions of the lawn.

Answer 1

Hint: As we know that the above given question is a word problem. A problem is a mathematical question written as one sentence or more describing a real life scenario where that problem needs to be solved by the way of mathematical calculation. We can solve the given problem by applying the method of mathematical equations and then solve them.

Complete step by step answer:
We need to first understand the requirement of the question which is the dimensions of the lawn or we can say that the side of the square. Let us draw a diagram representing the same with the path $4\,m$ wide and let the dimensions of the lawn be $x$ metres or $x$ m.

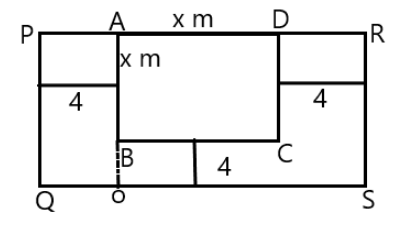
Here we have $ABCD$ is square lawn. And the path around it PQRS, which is a rectangle.In PQRS when we join the dotted line from B to O , then we get the length. Since we can see that the path is $4m$, so $BO = 4m$. As we can see the path around the square lawn is $4m$. We have assumed the side of the square lawn will be $x$ m. The area of the square is ${a^2}$, here we have $a = x$.So the area of the square lawn is ${x^2}{m^2}$.

We can see that the square lawn is bounded on three sides by a path which is $4m$ wide i.e. width of the path.We know that the length of the outer rectangle = length of the square $ + 2 \times $width of the path. It gives us the value $x + 2 \times 4 = x + 8$.Similarly breadth of the outer rectangle $ = $ length of the square + width of the path. By putting the values, we have $x + 4$.

We can now find the area of the outer rectangle i.e. area of rectangle = $length \times breadth$. We can write it as $(x + 4)(x + 8)$. Now we multiply and solve it: $x(x + 8) + 4(x + 8) = {x^2} + 8x + 4x + 32$. On adding the similar terms we have ${x^2} + 12x + 32$.From the above figure we can say that Area of the path = Area of the outer rectangle – area of the square lawn. So we put the values and we get the area i.e. ${x^2} + 12x + 32 - {x^2} = 12x + 32$.

According to the question area of the path $ = \,\dfrac{7}{8}$of the area of the lawn. By substituting the values we can write $12x + 32 = \dfrac{7}{8}{x^2}$.
On solving we have
$96x + 256 = 7{x^2}\\
 \Rightarrow 7{x^2} + 96x + 256$

We can solve the above quadratic equation by splitting the middle term, we get $7{x^2} - 112x + 16x - 256 = 0$.
We can take the common factors out,
$7x(x - 16) + 16(x - 16) = 0 \\
\Rightarrow (7x + 16)(x - 16) = 0$
Now we equate the values, $x - 16 = 0\,\,or\,7x + 16 = 0$.
It gives us the value $x = 16\,\,or\,\,x = - \dfrac{{16}}{7}$. We know that dimension can never be negative, so $x = - \dfrac{{16}}{7}$ is not possible.

Hence the required dimension of the square lawn is $x = 16\,m$.

Note:We should always be careful what the question is asking. Based on the requirement and by observing all the necessary information that is already available in the question we gather the information and then create an equation or by unitary method whichever is applicable, then we solve the problem and then verify the answer by putting the value in the problem and see whether we get the same answer or not.