Question

A square is not similar to a rectangle. Why?

Answer 1

Hint: First of all, try to recall what quadrilaterals are. Now think about squares and rectangles and from their differences, conclude that these two polygons are not similar.

Complete step-by-step answer:
In this question, we have to find out why square and rectangles are not similar.
Before proceeding with this question, let us see what a quadrilateral is. A quadrilateral is a plane figure that has four sides or edges and so it has four corners or vertices. A quadrilateral is shown below, where $\angle A+\angle B+\angle C+\angle D=360$.

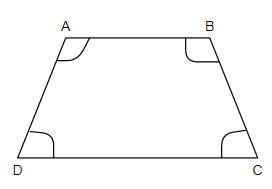
There are many types of quadrilaterals. As the word ‘Quad’ means four, all these types of a quadrilateral have four sides and the sum of angles of these shapes is 360 degrees. A few quadrilaterals are mentioned below.
1. Trapezium
2. Parallelogram
3. Square
4. Rectangle
5. Rhombus
6. Kite
Now, let us discuss squares and rectangles in detail.
Square: Square is a regular quadrilateral where all the four sides and angles are equal. All the four angles are right angles. Square is the most symmetrical quadrilateral we have.

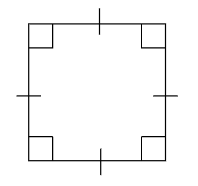
Area of the square is equal to the side squared that is, area = side2 per square unit. The perimeter of the square is equal to the sum of all its four sides, that is = 4 $\times $ side of the square.
Rectangle: A Rectangle is a four sided-quadrilateral. In a rectangle the opposite sides equal and all the internal angles are right-angled (90o).

A rectangle has length (l) and breadth (b). Both length and breadth are different in size. In the figure above we can see a rectangle ABCD with four sides, AB, BC, CD, and DA and right angles A, B, C, and D. The distance between A and B or C and D is taken as the length (l), whereas the distance between B and C or A and D is taken as the breadth (b) of the given rectangle. Area of the rectangle is its length multiplied by breadth that is, area = l $\times $ b. The perimeter of the rectangle is twice the sum of its length and breadth that is, perimeter = 2 (l + b).
Now let us consider our question. Let us see why squares and rectangles are not similar.
In the above discussion we have seen that squares have all the sides equal while in rectangle, all sides are not equal. We must note that in a rectangle the opposite sides are equal in length which makes it different from a square. Hence, squares and rectangles are not similar.

Note: In this question, students must note rectangles having equal length of adjacent sides are actually squares. We can also say that all squares are rectangles but we cannot say that all rectangles are squares. It is because a square satisfies all the conditions that rectangle does but converse is not true. Hence it is right to say that rectangles and squares are not similar.