Question

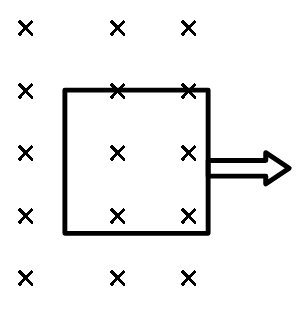
A square coil PQRS of resistance 2$\Omega$, 100 turns and side 10 cm is placed in a magnetic field = 2.0 T. The direction of the magnetic field is perpendicular to the plane of the coil as shown in Figure. The work done in pulling the coil completely out of the region of magnetic field in 2.0 s without any acceleration is

A. 0.01 J
B. 0.1 J
C. 1.0 J
D. 10 J

Answer 1

Hint: If a coil or conductor moves in a magnetic field an emf will be generated across its ends and the current will flow if the circuit is closed. The emf created will always oppose the cause (or motion) responsible for its creation. Therefore a work has to be done against this opposition.

Formula used:
If e is the emf generated in moving the coil then:
$Work = \dfrac{e^2}{R} \times time $

Complete step by step answer:
We know that power can be expressed by following relations:
$Power = \dfrac{Work}{time} $
$Power = VI$
where VI is the power for a circuit that has a supply of V and a current of I magnitude flowing in it.
'I' can be replaced by V/R and equating the two expressions for power give us:
$\dfrac{V^2}{R} = \dfrac{Work}{time}$
which can give us the expression for work done as:
$Work = \dfrac{V^2}{R} \times time $
When a square coil of side 10 cm with 100 turns is pulled out of a magnetic field completely in 2s, we can say that the flux change in it due to its motion will be given by:
$\dfrac{d \phi}{dt} = \dfrac{d(NBA)}{dt} $
B's constant area of a square is $(side)^2$ where one of the sides is unaffected by the motion let us call it l and another is along the direction of velocity let us call x (top and bottom sides).
We can write the area of our square as A = lx. As we substitute this back in the formula we get:
$e = NBl \times \dfrac{d(x)}{dt} $
The rate of change of flux gives us the magnitude of the emf generated.
Now, we are given that in the duration of 2s, the loop is completely pulled out of the field. If we assume that before 2s, the loop was in the field with its end towards the boundary of the field, then a length x = 10 cm gets pulled out in 2 seconds. So we may write:
$\dfrac{dx}{dt} = \dfrac{0.1}{2} $ = 0.05 m/s

Therefore keeping the given values we get the emf induced in the coil as:
$e = 100 \times 2 T \times 0.1 m \times 0.05 m/s$ = 1V.
Therefore the work done will be (by the use of formula)
$Work = \dfrac{(1V)^2}{2 \Omega} \times 2s $ = 1 J.
Therefore done in pulling out the coil from the magnetic field is 1.0 J so option (C) is the correct answer.

Note:
The formula for magnetic flux of a coil with N turns that is oriented at an angle $\theta $ with the magnetic field is given by $\phi = NBA \cos \theta$. The $\theta$ is the angle that the normal direction to the coil makes with the magnetic field. In the question, the magnetic field was perpendicular to the plane of the coil therefore in our case the $\theta$ was $0^{\circ}$. Therefore we simply used NBA to describe the flux of the magnetic field through the coil.