Question

A spherical shell of radius $R$ and uniformly charged with charge $Q$ is rotating about its axis with frequency $f$. Find the magnetic moment of the sphere?

Answer 1

Hint:We have given a spherical shell of radius $R$ with uniform charge Q . let it rotate around the z-axis. Let Angular velocity be $\omega $ and frequency is given $f$ . For solving this we should know the area of a sphere $\left( {4\pi {r^2}} \right)$ , spherical polar coordinates. We will divide the sphere into a small ring and then integrate it to find the magnetic moment of the sphere.

Complete step by step answer:
A uniformly charged solid sphere of radius $R$ carries a total charge $Q$ .

So surface charge density will be $\sigma = \dfrac{Q}{A}$ where $A$ is the volume of the sphere
 $\sigma = \dfrac{Q}{{4\pi {r^2}}}$
It rotates about its axis with a frequency $ = f$
let its angular velocity $\omega = 2\pi f$
Suppose the angular velocity $\overrightarrow \omega = \omega \widehat z$
To find the magnetic moment of the sphere we can divide the sphere into small charges.
Using spherical polar coordinates $\left( {\rho ,\phi ,\theta } \right)$ with origin at the center of the spherical shell, we consider a small area $dS$ of a circular ring of small width and radius $r$ located at a distance $R$ from the origin on the surface of the sphere.

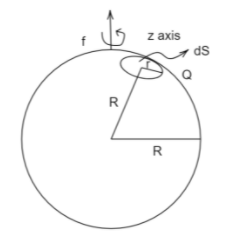
Here $\overrightarrow r = R\operatorname{Sin} \theta \widehat r$ and coordinate $\rho = R$ is constant for each elemental area.
 $dq = \sigma dS = \sigma {R^2}\sin \theta d\theta d\phi $
Current in the ring is given by
 $dI = dq \times f$
Using the value of $dq$and $f$ from above
 $dI = \dfrac{{\omega \sigma {R^2}\sin \theta d\theta d\phi }}{{2\pi }}$
The magnetic dipole moment of the ring is given by the expression in terms of the position vector $\overrightarrow r $ and current density $\overrightarrow J $ as
 \[d{\overrightarrow m _{ring}} = \dfrac{1}{2}\int\limits_{ring} {\overrightarrow r } \times \overrightarrow J \]
 \[ = \dfrac{1}{2}dI\int\limits_{ring} {\overrightarrow r } \times d\overrightarrow l \]
Where $d\overrightarrow l $ is the element length of the ring.
Line integral becomes equal to the circumference of the ring $ = 2\pi r\sin \theta $
 $ = dI(\pi {r^2}{\sin ^2}\theta )\widehat z$
Inserting value of $dI$ in above
 $d\overrightarrow m = \dfrac{{\overrightarrow \omega \sigma {R^4}{{\sin }^3}\theta d\theta d\phi }}{2}$
The total magnetic dipole moment is then
 $\overrightarrow m = \dfrac{{\overrightarrow \omega \sigma {R^4}}}{2}\int\limits_0^\pi {{{\sin }^3}\theta d\theta \int\limits_0^{2\pi } {d\phi } } $
 $\overrightarrow m = \dfrac{{\overrightarrow \omega \sigma {R^4}}}{2} \times \dfrac{4}{3} \times 2\pi $
 $\overrightarrow m = \dfrac{4}{3}\pi \sigma {R^4}\overrightarrow \omega $
We have to write in terms of $Q$
So, $\overrightarrow m = \dfrac{4}{3}\pi \left( {\dfrac{Q}{{4\pi {R^2}}}} \right){R^4}\overrightarrow \omega $
 $\overrightarrow m = \dfrac{Q}{3}{R^2}\overrightarrow \omega $
This is the required solution.

Note:Using spherical polar coordinates, we can take $dq = \rho d\tau = \rho {r^2}dr\sin \theta d\theta d\phi $, with the contribution to the dipole moment given by $d\overrightarrow m = \dfrac{1}{2}\overrightarrow r \times \overrightarrow J d\tau $ . One method would be to write down the volume integral directly, using $\overrightarrow J = \rho \overrightarrow \nu = \rho \overrightarrow \omega \times \overrightarrow r $ . Where $\rho $is volume charge density $\rho = \dfrac{Q}{V} = \dfrac{Q}{{\dfrac{4}{3}\pi {r^3}}}$
It is easy to see that if an electrically charged body is stationary, then this entire expression vanishes since $J = 0$ everywhere.