Question

A sound wave of frequency n travels horizontally to the right with speed c. It is reflected from a broad wall moving to the left with speed v. The number of beats heard by a stationary observer to the left of the wall is
                               

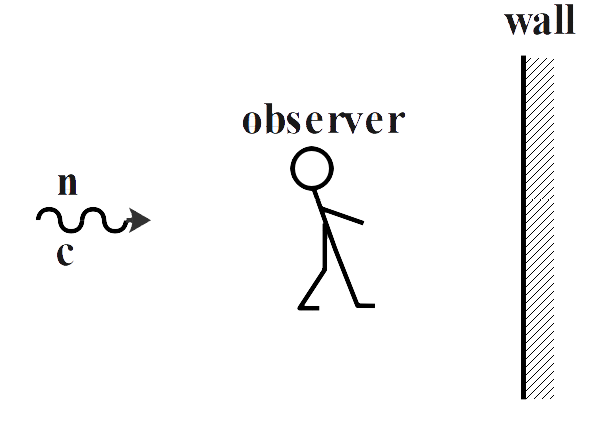
A. zero
B. \[\dfrac{n(c+v)}{c-v}\]
C. \[\dfrac{nv}{c-v}\]
D. \[\dfrac{2nv}{c-v}\]

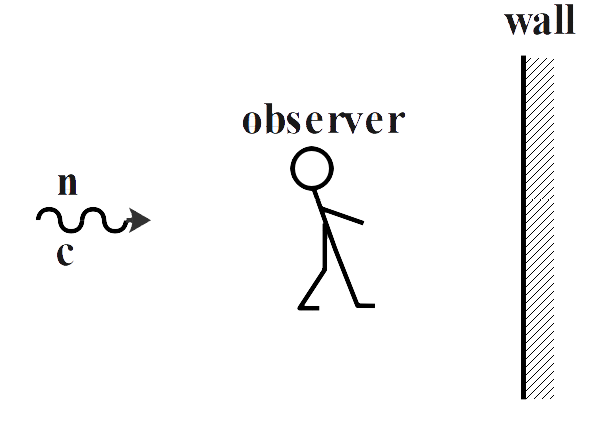
Answer 1

Hint: It is given that a sound wave is travelling with frequency n with speed c. It is reflected from a wall moving to the left with speed v. and the observer is between the wall and the sound wave source as shown in the diagram. We can see that this phenomenon represents the Doppler’s effect. Therefore, to calculate the number of beats we shall first calculate the frequency of sound reaching the wall and frequency received by a stationary observer after reflecting from the wall. We know that the difference of two calculated frequencies is the number of beats heard by an observer.

Formula used: \[f'=f\left( \dfrac{v\pm {{v}_{o}}}{v\pm {{v}_{s}}} \right)\]
Where,
f’ is the observer frequency of sound
f is the actual frequency of sound
v is the speed of sound in air
\[{{v}_{o}}\]is the observer velocity
\[{{v}_{s}}\]is the source velocity

Complete step by step solution:
when the sound wave is moving to the right as shown it will hit the wall. Therefore, the wall will now act as the observer. The speed of the wall is given as v. it is assumed that the actual sound source is stationary.
Now, to calculate the frequency of sound reaching the wall say \[{{n}_{1}}\]
Therefore, using formula
\[f'=f\left( \dfrac{v\pm {{v}_{o}}}{v\pm {{v}_{s}}} \right)\]
After substituting the given values
We get,
\[{{n}_{1}}=n\dfrac{c+v}{c}\] ………………….. (1)
Now, when the sound wave is reflected from the wall, the wall will act as a moving source with velocity v. this sound wave will now be heard by stationary observer.
Therefore, frequency received by stationary observer say \[{{n}_{2}}\] will be given by,
\[{{n}_{2}}={{n}_{1}}\dfrac{c+v}{c}\] …………………. (2)
From (1) and (2)
We get,
\[{{n}_{2}}=n\dfrac{c+v}{c-v}\] ……………….. (3)
Now, the direct frequency or number of beats heard by the observer will be given by,
\[x={{n}_{2}}-n\]
Substituting from (3)
We get,
\[x=n\dfrac{c+v}{c-v}-n\]
On solving,
\[x=\dfrac{2nv}{c-v}\]

So, the correct answer is “Option D”.

Note: The change in frequency of the wave in relation to an observer which is moving relative to source is given by the Doppler’s effect. An everyday example of doppler’s effect is the sound of a siren or a car moving past a stationary observer. The high pitch sound is heard when the car is approaching the observer and low pitch when the car is moving away from the observer.