
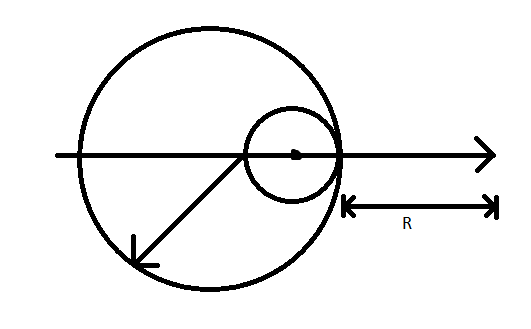
A solid sphere of uniform density and radius $R$ applies a gravitational force of attraction equal to ${{F}_{1}}$ on a particle placed at a distance $2R$ from the centre of the sphere. A spherical cavity of radius $R/2$ is now made in the sphere as shown in the figure. The sphere with the cavity now applies a gravitational force ${{F}_{2}}$ on the same particle. The ratio ${{F}_{1}}/{{F}_{2}}$ is

Answer
598.8k+ views
Hint: This problem can be solved by first finding out the gravitational force due to the sphere at the distance and then finding the gravitational force due to the sphere in the cavity by considering the cavity as a body of negative mass and subtracting the gravitational force due to this negative mass from the gravitational force due to the full sphere. Therefore, we can get the two forces and find out the required ratio.
Formula used:
The magnitude of the attractive gravitational force ${{F}_{g}}$ exerted by a mass $M$ on another mass $m$ is given by
${{F}_{g}}=\dfrac{GMm}{{{R}^{2}}}$
where $R$ is the distance between the centres of the two bodies and $G=6.67\times {{10}^{-11}}{{m}^{3}}k{{g}^{-1}}{{s}^{-2}}$ is the universal gravitational constant.
This force attracts the body of mass $m$ towards the centre of the body of mass $M$.
The volume $V$ of a sphere of radius $R$ is given by
$V=\dfrac{4}{3}\pi {{R}^{3}}$
Complete step by step answer:
As explained in the hint, we will first find the gravitational force due to the full sphere and then find the gravitational force due to the sphere with the cavity by subtracting the gravitational force due to the cavity (which we will consider as a negative mass) from the gravitational force due to the full sphere.
Now, let us consider the mass of the particle at the point to be of unit mass $m=1kg$ to ease our calculations.
Now, let the density of the sphere be $\rho $.
The radius of the full sphere is $R$.
Let the mass of the full sphere be $M$.
Let the volume of the full sphere be $V$.
The radius of the cavity is $R/2$.
Let the mass of the spherical cavity be ${{m}_{cavity}}$.
Let the volume of the spherical cavity be ${{V}_{cavity}}$
The volume $V$ of a sphere of radius $R$ is given by
$V=\dfrac{4}{3}\pi {{R}^{3}}$ --(1)
Now, $\text{Mass = Volume}\times \text{Density}$ --(2)
Therefore, using (1) and (2),
we get the mass of the full sphere $M$ as
$M=V\times \rho $
$\therefore M=\dfrac{4}{3}\pi {{R}^{3}}\rho $ --(3)
Now, we get the mass of the cavity as
${{m}_{cavity}}={{V}_{cavity}}\times \left( -\rho \right)$ (Since, it is a cavity, we have considered negative density)
$\therefore {{m}_{cavity}}=\dfrac{4}{3}\pi {{\left( \dfrac{R}{2} \right)}^{3}}\left( -\rho \right)=-\dfrac{4}{3}\pi \dfrac{{{R}^{3}}}{8}\rho $ ---(4)
The magnitude of the attractive gravitational force ${{F}_{g}}$ exerted by a mass $M$ on another mass $m$ is given by
${{F}_{g}}=\dfrac{GMm}{{{R}^{2}}}$ --(5)
where $R$ is the distance between the centres of the two bodies and $G=6.67\times {{10}^{-11}}{{m}^{3}}k{{g}^{-1}}{{s}^{-2}}$ is the universal gravitational constant.
This force attracts the body of mass $m$ towards the centre of the body of mass $M$.
Therefore, using (5), we will get the gravitational force on the particle of unit mass at the required point as
${{F}_{1}}=\dfrac{GM\left( 1 \right)}{{{\left( 2R \right)}^{2}}}=\dfrac{GM}{4{{R}^{2}}}$ --(6)
Now, the gravitational force due to the sphere with the cavity on the particle of unit mass at the required point will be the sum of the gravitational force due to the full sphere and that due to the cavity (which will be negative in magnitude)
$\therefore {{F}_{2}}=\dfrac{GM\left( 1 \right)}{{{\left( 2R \right)}^{2}}}+\dfrac{G{{m}_{cavity}}\left( 1 \right)}{{{\left( \dfrac{R}{2}+R \right)}^{2}}}=\dfrac{GM}{4{{R}^{2}}}+\dfrac{G{{m}_{cavity}}}{{{\left( \dfrac{3R}{2} \right)}^{2}}}=\dfrac{GM}{4{{R}^{2}}}+\dfrac{G{{m}_{cavity}}}{\dfrac{9{{R}^{2}}}{4}}=\dfrac{GM}{4{{R}^{2}}}+\dfrac{4G{{m}_{cavity}}}{9{{R}^{2}}}$ --(7)
$\left( \because {{F}_{cavity}}=\dfrac{G{{m}_{cavity}}\left( 1 \right)}{{{\left( \dfrac{R}{2}+R \right)}^{2}}} \right)$ , where ${{F}_{cavity}}$ is the gravitational force due to the cavity on the particle of unit mass at the required point. From the figure and the question, it is evident that the distance between the centre of the cavity and the particle is $\dfrac{R}{2}+R$. ]
Now, putting (3) in (6), we get,
${{F}_{1}}=\dfrac{G}{4{{R}^{2}}}\times \dfrac{4}{3}\pi {{R}^{3}}\rho =\dfrac{G\pi R\rho }{3}$ --(8)
Now, putting (3) and (4) in (7), we get,
$\begin{align}
& {{F}_{2}}=\left( \dfrac{G}{4{{R}^{2}}}\times \dfrac{4}{3}\pi {{R}^{3}}\rho \right)+\left( \dfrac{4G}{9{{R}^{2}}}\times \left( -\dfrac{4}{3}\pi \dfrac{{{R}^{3}}}{8}\rho \right) \right) \\
& =\dfrac{G\pi R\rho }{3}+\left( -\dfrac{2G\pi R\rho }{27} \right)=\dfrac{G\pi R\rho }{3}-\dfrac{2G\pi R\rho }{27}=\dfrac{9G\pi R\rho -2G\pi R\rho }{27}=\dfrac{7G\pi R\rho }{27} \\
\end{align}$ --(9)
Therefore, the required ratio ${{F}_{1}}/{{F}_{2}}$ is
$\dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{\dfrac{G\pi R\rho }{3}}{\dfrac{7G\pi R\rho }{27}}=\dfrac{27\times G\pi R\rho }{3\times 7G\pi R\rho }=\dfrac{9}{7}$.
Hence, the required ratio is $\dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{9}{7}$.
Note: It does not matter what value of the mass of the particle at the point we consider, since, it will anyway get cancelled out while writing the final answer in the form of a ratio. However, to avoid another unnecessary variable and make the calculations simpler, we consider the particle to be of unit mass. In such questions, where the final answer is in the form of a ratio, it is best not to go into extensive calculation for each individual quantity but write it in the form of variables as they have a chance of getting cancelled in the end. For example, we did not take the constant value of $G$ and plug it in the calculations as it got cancelled in the end anyway. If we had plugged in the value, it would have only further complicated our calculations.
Students get confused about how to solve problems involving a cavity. The best approach to solving such types of problems is to consider the cavity as a theoretical negative mass with negative material density. In this way we can find out the effect of the cavity easily.
Formula used:
The magnitude of the attractive gravitational force ${{F}_{g}}$ exerted by a mass $M$ on another mass $m$ is given by
${{F}_{g}}=\dfrac{GMm}{{{R}^{2}}}$
where $R$ is the distance between the centres of the two bodies and $G=6.67\times {{10}^{-11}}{{m}^{3}}k{{g}^{-1}}{{s}^{-2}}$ is the universal gravitational constant.
This force attracts the body of mass $m$ towards the centre of the body of mass $M$.
The volume $V$ of a sphere of radius $R$ is given by
$V=\dfrac{4}{3}\pi {{R}^{3}}$
Complete step by step answer:
As explained in the hint, we will first find the gravitational force due to the full sphere and then find the gravitational force due to the sphere with the cavity by subtracting the gravitational force due to the cavity (which we will consider as a negative mass) from the gravitational force due to the full sphere.
Now, let us consider the mass of the particle at the point to be of unit mass $m=1kg$ to ease our calculations.
Now, let the density of the sphere be $\rho $.
The radius of the full sphere is $R$.
Let the mass of the full sphere be $M$.
Let the volume of the full sphere be $V$.
The radius of the cavity is $R/2$.
Let the mass of the spherical cavity be ${{m}_{cavity}}$.
Let the volume of the spherical cavity be ${{V}_{cavity}}$
The volume $V$ of a sphere of radius $R$ is given by
$V=\dfrac{4}{3}\pi {{R}^{3}}$ --(1)
Now, $\text{Mass = Volume}\times \text{Density}$ --(2)
Therefore, using (1) and (2),
we get the mass of the full sphere $M$ as
$M=V\times \rho $
$\therefore M=\dfrac{4}{3}\pi {{R}^{3}}\rho $ --(3)
Now, we get the mass of the cavity as
${{m}_{cavity}}={{V}_{cavity}}\times \left( -\rho \right)$ (Since, it is a cavity, we have considered negative density)
$\therefore {{m}_{cavity}}=\dfrac{4}{3}\pi {{\left( \dfrac{R}{2} \right)}^{3}}\left( -\rho \right)=-\dfrac{4}{3}\pi \dfrac{{{R}^{3}}}{8}\rho $ ---(4)
The magnitude of the attractive gravitational force ${{F}_{g}}$ exerted by a mass $M$ on another mass $m$ is given by
${{F}_{g}}=\dfrac{GMm}{{{R}^{2}}}$ --(5)
where $R$ is the distance between the centres of the two bodies and $G=6.67\times {{10}^{-11}}{{m}^{3}}k{{g}^{-1}}{{s}^{-2}}$ is the universal gravitational constant.
This force attracts the body of mass $m$ towards the centre of the body of mass $M$.
Therefore, using (5), we will get the gravitational force on the particle of unit mass at the required point as
${{F}_{1}}=\dfrac{GM\left( 1 \right)}{{{\left( 2R \right)}^{2}}}=\dfrac{GM}{4{{R}^{2}}}$ --(6)
Now, the gravitational force due to the sphere with the cavity on the particle of unit mass at the required point will be the sum of the gravitational force due to the full sphere and that due to the cavity (which will be negative in magnitude)
$\therefore {{F}_{2}}=\dfrac{GM\left( 1 \right)}{{{\left( 2R \right)}^{2}}}+\dfrac{G{{m}_{cavity}}\left( 1 \right)}{{{\left( \dfrac{R}{2}+R \right)}^{2}}}=\dfrac{GM}{4{{R}^{2}}}+\dfrac{G{{m}_{cavity}}}{{{\left( \dfrac{3R}{2} \right)}^{2}}}=\dfrac{GM}{4{{R}^{2}}}+\dfrac{G{{m}_{cavity}}}{\dfrac{9{{R}^{2}}}{4}}=\dfrac{GM}{4{{R}^{2}}}+\dfrac{4G{{m}_{cavity}}}{9{{R}^{2}}}$ --(7)
$\left( \because {{F}_{cavity}}=\dfrac{G{{m}_{cavity}}\left( 1 \right)}{{{\left( \dfrac{R}{2}+R \right)}^{2}}} \right)$ , where ${{F}_{cavity}}$ is the gravitational force due to the cavity on the particle of unit mass at the required point. From the figure and the question, it is evident that the distance between the centre of the cavity and the particle is $\dfrac{R}{2}+R$. ]
Now, putting (3) in (6), we get,
${{F}_{1}}=\dfrac{G}{4{{R}^{2}}}\times \dfrac{4}{3}\pi {{R}^{3}}\rho =\dfrac{G\pi R\rho }{3}$ --(8)
Now, putting (3) and (4) in (7), we get,
$\begin{align}
& {{F}_{2}}=\left( \dfrac{G}{4{{R}^{2}}}\times \dfrac{4}{3}\pi {{R}^{3}}\rho \right)+\left( \dfrac{4G}{9{{R}^{2}}}\times \left( -\dfrac{4}{3}\pi \dfrac{{{R}^{3}}}{8}\rho \right) \right) \\
& =\dfrac{G\pi R\rho }{3}+\left( -\dfrac{2G\pi R\rho }{27} \right)=\dfrac{G\pi R\rho }{3}-\dfrac{2G\pi R\rho }{27}=\dfrac{9G\pi R\rho -2G\pi R\rho }{27}=\dfrac{7G\pi R\rho }{27} \\
\end{align}$ --(9)
Therefore, the required ratio ${{F}_{1}}/{{F}_{2}}$ is
$\dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{\dfrac{G\pi R\rho }{3}}{\dfrac{7G\pi R\rho }{27}}=\dfrac{27\times G\pi R\rho }{3\times 7G\pi R\rho }=\dfrac{9}{7}$.
Hence, the required ratio is $\dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{9}{7}$.
Note: It does not matter what value of the mass of the particle at the point we consider, since, it will anyway get cancelled out while writing the final answer in the form of a ratio. However, to avoid another unnecessary variable and make the calculations simpler, we consider the particle to be of unit mass. In such questions, where the final answer is in the form of a ratio, it is best not to go into extensive calculation for each individual quantity but write it in the form of variables as they have a chance of getting cancelled in the end. For example, we did not take the constant value of $G$ and plug it in the calculations as it got cancelled in the end anyway. If we had plugged in the value, it would have only further complicated our calculations.
Students get confused about how to solve problems involving a cavity. The best approach to solving such types of problems is to consider the cavity as a theoretical negative mass with negative material density. In this way we can find out the effect of the cavity easily.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

What is the difference between biodegradable and nonbiodegradable class 11 biology CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE




